前回まででSVMの導入と計算方法は終わりました。
SVMの導入
bananarian.hatenablog.com
最適化問題を解く話
bananarian.hatenablog.com
しかし、前回までは頑なに
データをきれいに線形に分類できる、線形分離可能という仮定を置いていました。
これをハードマージンと呼びます。
ただ実際のデータはそんなにきれいな形をしていません。多少のミスくらいは許容してやる分類器を考えたって問題なさそうです。
この多少のミスは許すSVMをソフトマージンと呼びます。
今回はソフトマージンSVMの内、ラディアルカーネルSVMの実装についての話をします。
スポンサーリンク
ラディアルカーネルSVMのパラメータ
コストパラメータ:C
カーネルパラメータ:
の二つがあります。これについてですが、
Cは罰則です。この値が大きいほどミスを認めない分類器になります。
は複雑さに関するパラメータです。この値が大きいほど複雑な形で分類できます。小さいと前説明した通りの直線になります。
パラメータを変えて試してみる
では試しにRで実装して何が起こっているか確認してみます。
まず、試すために仮のデータセットを作ります。
#e1071パッケージを使う library(e1071) #標準正規分布に従うデータを200×2だけ2列分生成 x=matrix(rnorm(200*2), ncol=2); #最初の150個のデータを+2だけずらす x[1:150,]=x[1:150,]+2; #次の50個のデータを-2だけずらす x[151:200,]=x[151:200,]-2 #+2ずらしたものを1,-2ずらしたものを2と名前を付ける y=c(rep(1,150), rep(2,50)); #データの生成 dat=data.frame(x=x,y=as.factor(y)) plot(x, col=y)
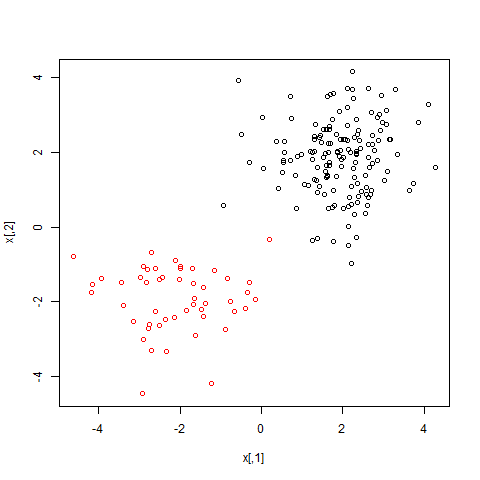
ラディアルカーネルSVMをこれに試してみます。
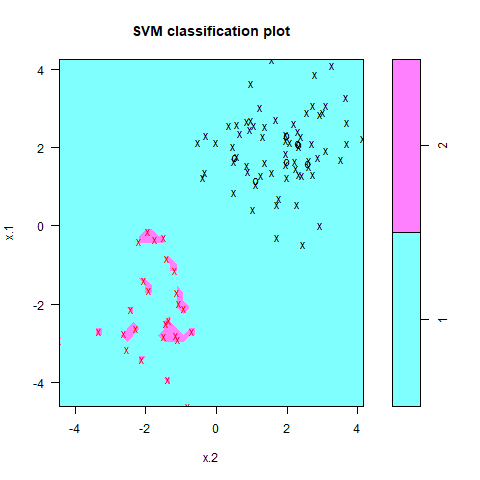
C=1,=1で分類してみます。
#100個適当に取り出して訓練データとする train=sample(200,100) #e1071パッケージのsvm関数を使う svmfit=svm(y~., data=dat[train,], kernel ="radial", gamma=1,cost=1) plot(svmfit, dat[train,])
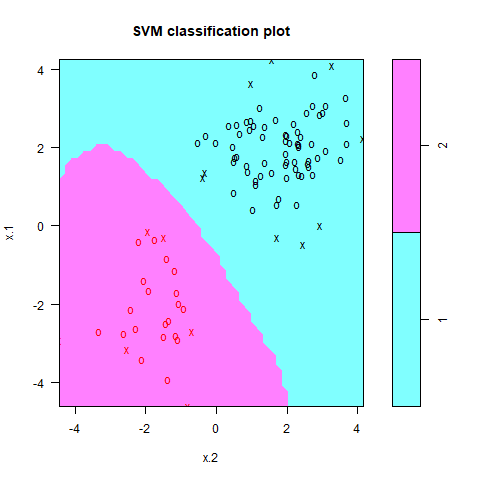
ちなみに×印はSVMを引くにあたって利用した境界に近い点です。これをサポートベクターと呼びます。
多少のミスを許したうえで赤いやつは赤いグループに分類できています。
ちなみに、=10に変えてみるとこんな感じです。複雑な分類器が出来ています。
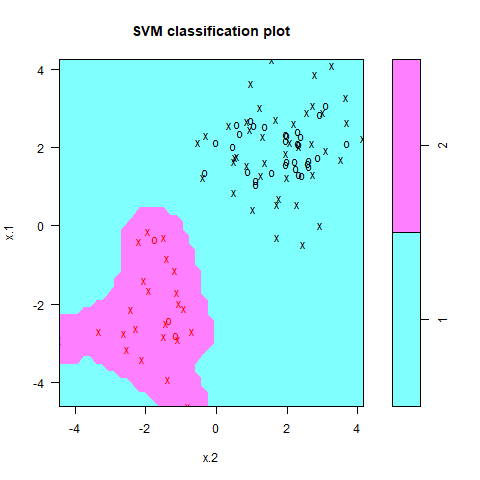
ここからC=0.01にしてみると次のようになります。
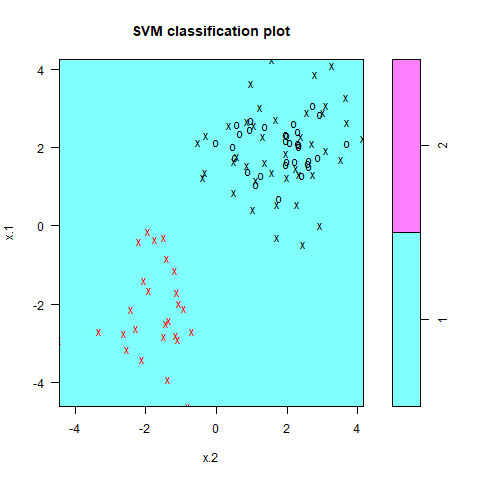
罰則が全く機能せず、全て青の領域に入ってしまっていることが分かります。
にしてみました。これはやりすぎですね。ここまでいくと過適合しすぎていて、新しいデータを加えた時に正しく分類してくれなさそうです。