前回、前々回は因子分析について、分析方法について学びました。
bananarian.hatenablog.com
bananarian.hatenablog.com
今回は実際のマーケットデータに応用してみます。
ただし、実際のデータは使えないので架空のデータを作って利用します。
架空のデータ
次のようなデータを作りました。
head(beer_data) Beer1 Beer2 Beer3 Beer4 Beer5 Beer6 Beer7 Beer8 Beer9 1 8 3 7 10 7 7 7 4 8 2 7 3 8 3 4 9 9 7 4 3 9 2 9 5 7 10 6 8 7 4 2 7 4 10 7 6 7 7 3 5 10 6 5 10 7 7 10 10 6 6 7 5 6 9 6 4 10 10 9 dim(beer_data) [1] 200 9
これは、200人に対してとったアンケートの結果で、質問は次の通りです。
「Beer1からBeer9までのビールについて、1から10でどれくらい買いたいと思うかに関する度合を教えてください。」

このデータから、消費者はどういった購買要因の下で購買を行っており、各ビールはどの要因に強く影響を受けて購入されているのかといったことを考えたいとします。
変数間の相関
前回の話では扱わなかったのですが、どうやら各変数の相関を見る際に、psychパッケージでは、下三角形だけ見せてくれる関数があるようです。今回はそれを使ってみました。
library("psych") library("GPArotation") lowerCor(beer_data) Beer1 Beer2 Beer3 Beer4 Beer5 Beer6 Beer7 Beer8 Beer9 Beer1 1.00 Beer2 -0.40 1.00 Beer3 0.37 -0.25 1.00 Beer4 0.22 -0.30 0.21 1.00 Beer5 0.02 -0.19 0.15 0.28 1.00 Beer6 0.08 -0.20 0.10 0.13 0.35 1.00 Beer7 0.28 -0.21 0.15 0.13 0.04 0.06 1.00 Beer8 0.31 -0.10 0.18 0.23 0.06 0.07 0.39 1.00 Beer9 0.22 -0.21 0.13 0.20 0.22 0.14 0.01 0.15 1.00
平行分析
前回はスクリープロットで要因数を決定しましたが、今回は平行分析という手法を使ってみます。
平行分析は、固有値の減少と乱数の列を比較して、切り替わったところで要因数を決定します。
これはfa.parallel関数により簡単にできます。
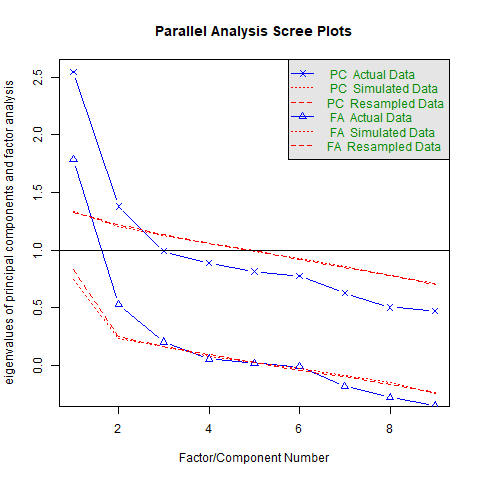
fa.parallel(beer_data,fm="ml")
×の線は主成分分析のプロットのため、今回は無視します。
△の線を見てください。3と4の間で乱数の線とぶつかりました。
そこから、今回は要因数は3と決定します。
結果の確認
> fa_beer=fa(beer_data,nfactors=3,fm="ml") > fa_beer Factor Analysis using method = ml Call: fa(r = beer_data, nfactors = 3, fm = "ml") Standardized loadings (pattern matrix) based upon correlation matrix ML2 ML1 ML3 h2 u2 com Beer1 0.78 0.05 -0.10 0.61 0.388 1.0 Beer2 -0.56 0.11 -0.20 0.37 0.633 1.3 Beer3 0.43 0.03 0.12 0.23 0.773 1.2 Beer4 0.25 0.12 0.33 0.24 0.764 2.2 Beer5 -0.04 0.01 0.77 0.59 0.410 1.0 Beer6 0.07 0.01 0.43 0.20 0.798 1.0 Beer7 0.24 0.31 -0.02 0.21 0.794 1.9 Beer8 0.00 1.00 0.01 1.00 0.005 1.0 Beer9 0.22 0.06 0.25 0.15 0.854 2.1
要因ML2を強く持つ人は、Beer1とBeer3は好きだけども、Beer2は嫌いであることが予測できます。
実際の分析では、それぞれのビールの味や種類が大体わかるので、
要因1はコクとキレに関する要因だな、とか要因2はフルーツベースかどうかだな
とかいったように考えることが出来ます。
また、各要因の相関も見てみると、
With factor correlations of
ML2 ML1 ML3
ML2 1.00 0.35 0.19
ML1 0.35 1.00 0.07
ML3 0.19 0.07 1.00
このようになりました。ML2とML1は若干相関があるので、ML2の要素を持つビールが好きな消費者はML1を持つビールも好きという傾向が若干あると言うこともできます。