単純パーセプトロンとマージンに関するまとめ

今日は単純パーセプトロンの話をします。
実際の現場で役に立っているのは多層パーセプトロンや、SVMですが、その基礎となるパーセプトロンについて理解しておくことは重要ですので、とりあえず一通りまとめていきます。

単純パーセプトロンとは何か
数学的な理解
パラメータの探索
マージンに関する話
重要定理について
- Novikovの定理
- Freund and Schapire の定理
  - マージンスラック変数
  - 定理詳細
今回の記事の話に関する機械学習関連のおすすめ図書

単純パーセプトロンとは何か

まず、単純パーセプトロンとはなんですか？って話をしておきます。

簡単にいうと、「直線(超平面)を引っ張って、空間を二つに分けることで、２クラス分類をやろう」というのがこの手法にあたります。
簡単な例を示すとこんな感じ。

f:id:bananarian:20190802215915p:plain

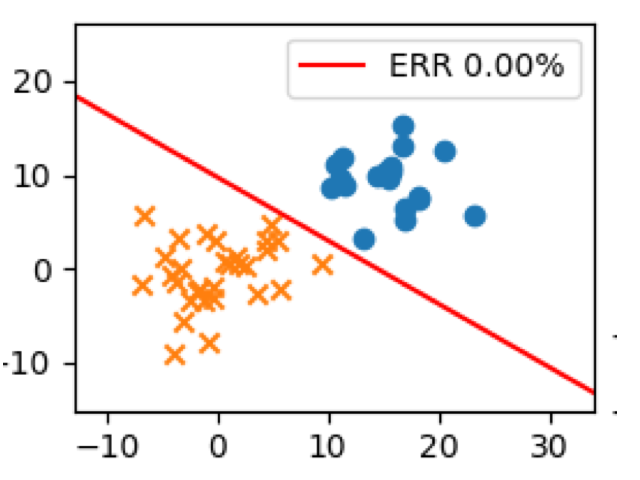
２つの領域に分けて、うまいこと２種類のクラスに分類しています。

直線を引っ張るだけなら、線形回帰か？？と思われる方もいらっしゃるかもしれませんが、線形回帰とは違います。その辺の話も後でしようと思います。

数学的な理解

まず、適当な直線を考えましょう。未知パラメータベクトル $\omega=(\omega_0,...\omega_k)$ 、特徴量(統計の文脈で言うところの説明変数) $X_1,...X_k$ を用いて次のような直線を考えます。

$y=\omega_0+\omega_1 X_1+\cdots+\omega_k X_k$

気持ちとしては、直線の上側と下側でクラスが分かれると嬉しいので、次のような関数 $\phi$ をに突っ込みましょう。

$y≥0$ の時
$\phi(y) = 1$

$y<0$ の時
$\phi(y) = -1$

これで、yが実数範囲でどのような値を取ろうとも、1か-1かどちらかに分類することができます。
ちなみに、ここで１と−１にしている理由もしっかりあります。これは後々の解説で説明します。

さて、ここで $y≥0$ ですが、

$y=\omega_0+\omega_1 X_1+\cdots+\omega_k X_k$

でしたので、

$\omega_0+\omega_1 X_1+\cdots+\omega_k X_k≥0$ 、つまり $\omega_1 X_1+\cdots+\omega_k X_k≥-\omega_0$

変形後の左側の式は、切片0の直線です。このように見方を変えると、 $\omega_0$ はちょっと他の係数とは役割が異なり、領域の閾値を表していることがわかります。
そのため、機械学習の文脈では、この切片のことを特に他の係数と区別して、バイアス項と呼んだりもしています。

ここまで読めば、線形回帰との違いはわかりますよね。

数式的な観点で言えば
そもそも線形回帰とは違って誤差項を仮定しているわけではありませんし、確率的な変動も考えていません。
あくまで、２クラスに分類できると仮定して、直線を引っ張っているだけであることに注意してください。
(当然確率的な変動を考えて定式化することもできる)

モチベーション的な観点から見ても
線形回帰はデータ点が確率的な変動を伴いながら線形に並ぶことを想定した統計手法ですが、

単純パーセプトロンはデータを特徴量空間に並べた場合に、直線で二分することができるということを想定した分類アルゴリズムです。

パラメータの探索

パラメータ探索イントロ

さて、整理したところで、次にパラメータの値をどう決めようと言う問題にシフトすることにします。

統計学にせよ、機械学習にせよ、どんな値が尤もらしいかを考えて、パラメータの値を決めなければなりません。

言い方を変えると、パラメータの値を見つけるためには、妥当な、計算しやすい評価方法を考え、その方法を持って評価する必要があります。

さて、ここで次のようなデータが与えられているとしましょう。

f:id:bananarian:20190802225239p:plain

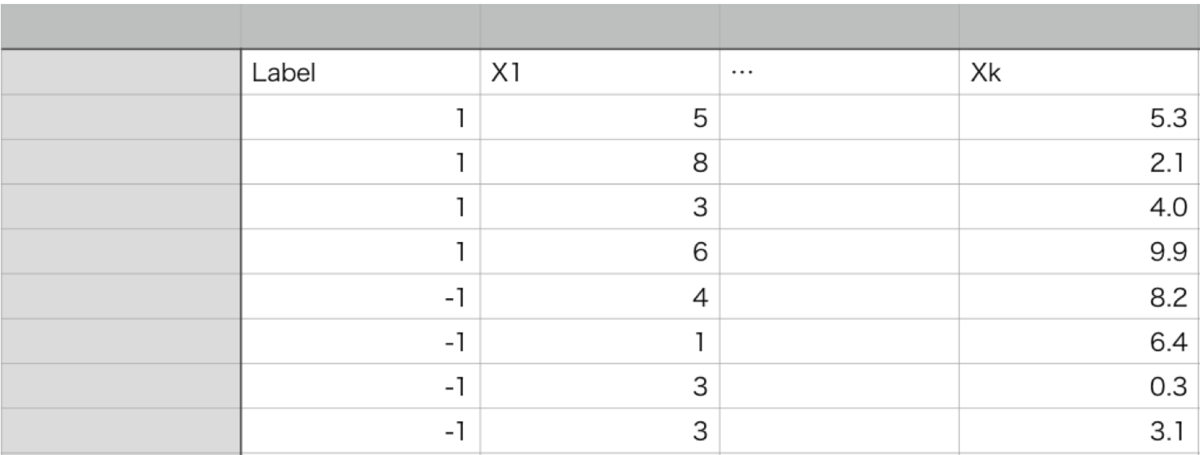
正解ラベルとしてLabel(1 or -1)が与えられているデータです。このデータを使って、２クラス分類のアルゴリズムを単純パーセプトロンを作り、例えば新しいデータがやってきたときに、特徴量を使って正しく分類したいと言ったことがモチベーションです。

そこで、まず問題になるのは

どんな値で評価しよう？？と言うことです。

パラメタ探索の評価

すぐ思いつくのは、

予測ラベル $\hat{\phi(y_i)}$ と、正解ラベル $Label_i$ を用いて評価関数Eを次のように設定すれば良いのではないか？ということです。

$E = \sum_{i=1}^n (\hat{\phi(y_i)} - Label_i)^2$

こうすれば、 $\hat{\phi(y_i)}$ が $Label_i$ が一致すれば0,不一致ならば $2^2$ となり、全て正しく分類できている場合に限り $E=0$ となります。

Eが極力小さくなるような $\omega$ を探せばいいじゃないか!めでたしめでたし

とはなりません。このEには欠陥があります。
Eは離散値しかとらないので、微分を使った最適化法が行えません。
とすると適当な離散最適化から攻めたり、データが少なければ総当たりという方法も考えられますが、やはり離散値では使い勝手がよくありません。

そこで、うまく離散値をとるような評価関数を考えます。

次のようなEを考えてみましょう。

$E = -\sum_{i=1}^n y_i Label_i 1_{(y_i Label_i<0)}$

ただし
$y_i = \omega_0+\omega_1 X_{(1,i)}+\cdots+\omega_k X_{(k,i)}$
$1_{(y_i Label_i<0)}$ は定義関数(指示関数)で、 $y_i Label_i<0$ の時に１、そうでないときに0をとる関数です。

ちなみに、 $y_i Label_i$ は各点における関数マージンとも呼ばれます。

こうすることで、誤差が出る場合には、Eは値が増え、正しい場合には0のまま、しかも連続的な値をとる関数と見ることができます。

このEを最小化(0に近づける)することを考えます。

パラメータの探索(確率的勾配法)

では、このEを $\omega$ で微分してみましょう。

$\frac{\partial E}{\partial \omega_s} = -\sum_{i=1}^n X_{(s,i)} Label_i 1_{(y_i Label_i<0)}$

ここで、勾配が0であれば適当な局所解であるはずです。

よって、とりあえず適当に $\omega$ の初期値として $\omega_0^{(0)},...\omega_k^{(0)}$ を与えて、そこから勾配に従って修正を行なっていきます。

つまり

$\omega^{(t)} = \omega^{(t-1)} + \frac{\partial E}{\partial \omega}$

これを繰り返していくことで、適切に分類できるパラメータ値に近づけていきます。

ここで、 $Label_i 1_{(y_i Label_i<0)}$ は次のように書いている本もあったりしますが、意味としては同じですね。

$(y_i - Label_i)$

こっちの方が見やすいので、以降は次のように書くことにします。

$\frac{\partial E}{\partial \omega} = -\sum_{i=1}^n X_{(s,i)} (y_i - Label_i)= \sum_{i=1}^n X_{(s,i)} ( Label_i-y_i)$

ということで、これで、探索アルゴリズムも完成しました。めでたしめでたし。

より効率の良い又は精度の良いアルゴリズム

例えば、 $X_1$ が20~30の範囲をとるような場合を考えます。この時、 $\omega$ の更新は20ほどの値を足したり引いたりして近づいていくことになりますが、この更新の値幅って20より2の方が正確だし、2より0.2の方がより正確な値を探すことができるはずですよね。

ただし一方で、この値が細かくなればなるほど収束時間が長くなるはずですね。

つまり、この更新幅は調整出来たようが嬉しいわけです。

ということで、先ほどのアルゴリズムを少し改善して、次のように学習率 $\eta \in [0,1]$ を与えてみましょう。

$\omega^{(t)} = \omega^{(t-1)} + \eta \frac{\partial E}{\partial \omega}$

この学習率を適当な値に変えて、収束するパラメータを探していくというアルゴリズムになるわけです。

マージンに関する話

関数マージン

データ点関数マージン

先ほど出てきたマージンについてもう少し考えてみることにします。

今、与えられているデータとして $(X_i,Label_i)$ がありますが、
※特徴量は以下 $X_i$ というベクトルの形でまとめて表記し直す。
$X_i = (X_{(1,i)},...X_{(k,i)})^{'}$

この時、あるパラメータ $\omega=(\omega_1,...\omega_k)$ とバイアスパラメータ $\omega_0$ を使って、次のような直線(超平面)を引くのでした。

$\omega X_i +\omega_0$

さらに、先ほどちらっと出てきましたが次のような $\gamma_i$ をデータiに対する関数マージンと呼んでいました。

$\gamma_i = Label_i (\omega X_i +\omega_0)$

超平面関数マージン

さて、仮にパラメータ $\omega,\omega_0$ を適当な値に固定したとします。
そうすると、超平面は適当な値に固定されるわけですが、この場合、データ点で見たときの関数マージンはデータ点の個数分(つまり、今回ならn個)出てきます。

$\gamma_1,\cdots,\gamma_n$

このうち最小の値をとる関数マージン $min\{\gamma\}$ を超平面における関数マージンと呼びます。

幾何マージン

データ点幾何マージン

関数マージンだと、正直数式的には、そうですかと言った感じですが、直観的に何をやっているのかがわかりにくい。
そこで、次のようにデータ点における関数マージンを正規化してやることにします。

$\frac{\gamma_i}{||\omega||}$

これを、幾何マージンと呼びます。
分母はバイアスパラメータ以外のパラメータに関するノルムです。

これのどこがわかりやすいのかというと、絶対値を取れば、点と直線の公式になっていますよね？

つまり、正解率100%の超平面を引いた場合、幾何マージンは超平面と点の距離になっているということになります。
心なしかイメージしやすくなりました。

超平面の幾何マージン

関数マージンの場合と同様ですが、各データ点における幾何マージンのうち、最小の値をとる幾何マージンを、超平面における幾何マージンと呼びます。

最大マージン超平面

ここまでは、データ点を固定して、各点におけるマージンを見たり、超平面を固定したときに、特に小さいマージンを見たりしましたが、

実際の超平面は様々考えられます。

考えられうるすべての超平面における幾何マージンを考えてみましょう。
当然、分類に誤りがある超平面であれば、幾何マージンは負の値を取ります(各データ点における最小の幾何マージンが超平面の幾何マージンでした)。

一方、100％正解する超平面の複数考えられますが、その場合、一番近いデータ点からの距離が近ければ幾何マージンは小さくなりますし、離れていれば幾何マージンは大きくなります(実際にフリーハンドで描いてみるとわかりやすい)。

100%正解するのであれば、データ点スレスレの直線を引くよりも、余裕を持った直線を引いた方が良いですよね。

つまり、超平面の幾何マージンは大きい方が嬉しいわけです。

そこで、すべての、超平面の幾何マージンのうち、最大の値をとる幾何マージンを最大マージン超平面と名付けます。

当然ですが、線形分離可能なデータであれば、この最大マージン超平面は正の値を取ります。

重要定理について

さて、以下は一通り重要な定理を確認していきます。
共立出版のサポートベクターマシン入門が非常によくまとまっていて、そのまま証明を書くと丸写しになってしまうので、証明自体は本に譲ります。
ここでは、上の説明と結びつけながら、定理の意味について説明していきます。

若干和訳に難がありますが、非常に良い本ですので、副読本にオススメです。

Novikovの定理

ある、２クラスのデータが両方含まれるデータ集合(トレーニング集合)に対して、線形分離可能を仮定する。
更に次の値 $R$ を考えます。

$R = max_{1≤i≤n} ||X_i||$

ここで、すべてのiについて、 $||\omega_{opt}||=1$ で、更に

$Label_i (\omega_{opt} X_i+\omega_0)≥\gamma$

※ただし $\gamma$ は既に与えている分離超平面におけるマージン

が成り立つような $\omega_{opt}$ が存在すると仮定します。
つまり、より良い超平面(または同等)が存在するという仮定です。

このとき、このデータ集合について、パーセプトロンアルゴリズムが失敗する数は高々

$(\frac{2R}{\gamma})^2$

に抑えられることがわかります。

これがNovikovの定理です。

気持ちとしては、線形分離可能であるならば、アルゴリズムが失敗する回数の上限がこの数で抑えられるので、高々有限回の試行で収束するという保証です。

更に、気になる点としては、失敗の上限は学習率に依存しないというところですね。

Freund and Schapire の定理

マージンスラック変数

この定理では、線形分離不可能な場合はどう考えるんだという疑問に対する解答が与えられます。
線形分離不可能な場合、マージンで考えるのは難しいので、新たな概念としてマージンスラック変数 $\xi$ を導入します。

超平面に対するマージンを $\gamma>0$ として固定する。これを以下ターゲットマージンと呼ぶ。
このとき、各点が超平面からこのターゲットマージンを持つにあたって、どの程度失敗しているかを $\xi_i$ として定量化する。

$\xi_i((X_i,Label_i), (\omega,\omega_0),\gamma) = max\{0, \gamma-Label_i (\omega X_i +\omega_0) \}$

これをマージンスラック変数と呼ぶことにします。

定理詳細

重複もなく、２クラスのデータが含まれたデータ集合に対して、||X_i||≤Rとする。
更に $(\omega,\omega_0)$ を $||\omega||=1$ を満たす任意の超平面とする。
$\gamma>0$

このとき、変数Dを次のように定義する。

$D = \sqrt{\sum_{i=1}^n \xi((X_i,Label_i),(\omega,omega_0),\gamma )^2}$

このとき、パーセプトロンアルゴリズムの最初の１回目の実行での失敗の数は高々

$(\frac{2(R+D)}{\gamma})^2$

になる。

つまり、線形分離不可能なデータ集合では、最終的にアルゴリズムの結果が振動して、収束しないわけだが、そうは言っても最初の１回の試行における失敗の数は上限があると、この定理から述べることができるわけです。

今回の記事の話に関する機械学習関連のおすすめ図書

サポートベクターマシン入門

ITエンジニアのための機械学習理論入門

パターン認識と機械学習　上

Python機械学習プログラミング