負の二項分布の最尤推定量 - バナナでもわかる話

せっかく前回負の二項分布に関する記事を上げたので、成功回数を固定した時の成功率に関する最尤推定量を求めてみます。
負の二項分布とRのrnbinom関数は何を表すのか - バナナでもわかる話

ちなみに最尤推定量についてはこちら
基礎からイメージで学ぶ統計学~最尤推定量編~ - バナナでもわかる話

負の二項分布の確率質量関数の確認

負の二項分布の確率質量関数はこんな感じでした。
$P(X;p,r)=\frac{(X-1)!}{(X-1-r)!r!}p^r(1-p)^{(X-r)}$

独立同一に負の二項分布に従う確率変数 $X_1,...X_m$ の同時分布は掛け算すればいいだけなので次のようになりますね。

$\prod_{i=1}^{m}\{\begin{eqnarray*} && {}_{X_i-1} C _r \end{eqnarray*}p^r(1-p)^{X_i-r}\}$

負の二項分布の最尤推定量の導出

まず、対数尤度関数は次のようになりますね。
$L(p;r,X)=log[\prod_{i=1}^{m}\{\begin{eqnarray*} && {}_{X_i-1} C _r \end{eqnarray*}p^r(1-p)^{X_i-r}\}]$
$=\sum_{i=1}^{m}log(\begin{eqnarray*} && {}_{X_i-1} C _r \end{eqnarray*})+mrlog(p)+\{log(1-p)\}\sum_{i=1}^{m}(X_i-r)$

$p$ で微分してやります。

$\frac{\partial L(p;r,X)}{\partial p}=mr-p\{mr+\sum_{i=1}^{m}(X_i-r)\}=0$

を満たすような $p$ の推定量 $\hat{p}$ は次のようになりますね。

$\hat{p}=\frac{r}{r+\bar{X}-\frac{r}{m}}$

Rでチェック

最尤推定量であれば、一致性が成り立つはずなので、サンプルサイズさえ大きくすれば大数法則で真の値に近づくはずです。
f:id:bananarian:20181013032933p:plain

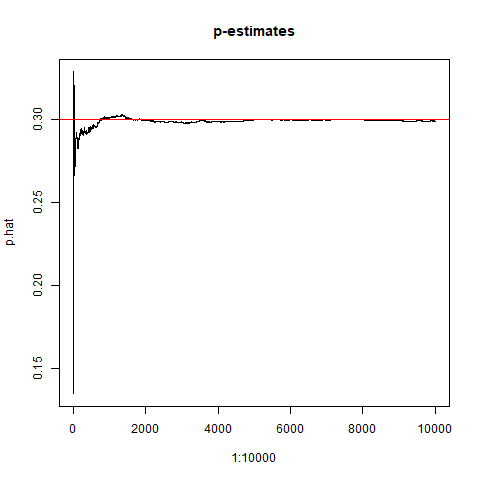
コードはこんな感じ

data=vector()
p.hat=vector()
for(i in 1:10000){
	data[i]=rnbinom(n=1, size=5, prob=0.3)
	mean=mean(data)
	p.hat[i]=5/(5+mean-5/i)
}
plot(1:10000,p.hat,main="p-estimates",type="l")
abline(0.3,0,col="red")