期待値の無いコーシー分布の平均を取ると何が起こるか

コーシー分布と言う分布があります。

この分布ですが、裾が厚いため、広い範囲で値を取り、期待値の無い分布であると言われます。

仕組み的には要はバラバラと外れ値のような値を取るため、期待値が収束しないわけなのですが、

本当か？というのをシミュレーションで確認してみようと思います。

もし、本当であれば平均をとっても値が大きくバラつくはずですね。

Rを使ったシミュレーション

ちなみに、コーシー分布ですが、パラメータは二つあって、中央値を示すlocationパラメータと、形を決めるscaleパラメータです。
Rのコードとしては

rcauchy(n,location,scale)

を利用します。

mean_seq=vector()

for(i in 1:1000){
	data=rcauchy(1000,location=0,scale=1)
	mean_seq[i]=mean(data)
}
plot(mean_seq)

1000個とりだして、平均をプロットしてみました。

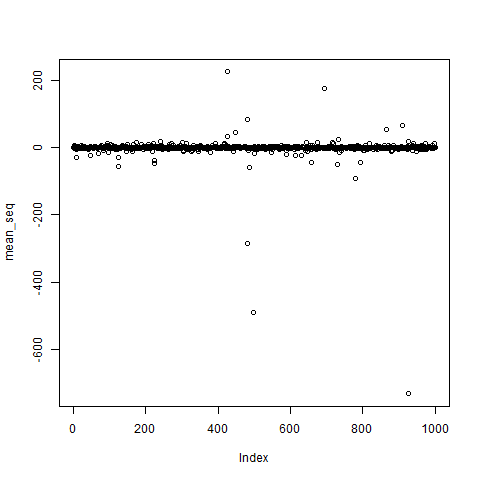
明らかに変なところにすっ飛んでいっている平均値が結構ありますね。一応サンプルサイズは1000あるので、この現象は普通はあり得ないと思います。
試しに、正規分布で同じことをしてみると....

mean_seqnorm=vector()

for(i in 1:1000){
	data=rnorm(1000,0,1)
	mean_seqnorm[i]=mean(data)
}
plot(mean_seqnorm)

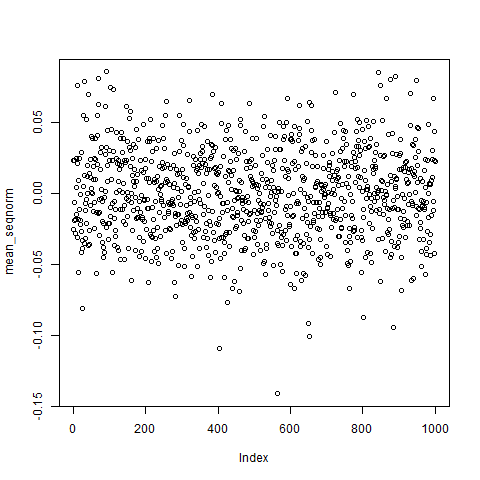
極端に外れた値は取らず0の周りに固まっています。
算術平均がきちんと期待値に収束している証拠ですね。

ちなみにコーシー分布は中央値は存在します。

中央値で同じことをやってやると次の通り。

med_seq=vector()

for(i in 1:1000){
	data=rcauchy(1000,location=0,scale=1)
	med_seq[i]=median(data)
}
plot(med_seq)

コーシー分布はこのような性質があるからこそ、仕組み上外れ値が発生しうるデータのモデリングに使われたりします。