マルコフ連鎖の収束とRによる収束シミュレーション

前回の記事では、マルコフ連鎖の推移確率行列について、n個先の確率行列はチャップマンコルモゴロフ方程式を使って簡単に計算できるということを説明しました。
bananarian.hatenablog.com

しかし、この記事を読んでも、

「え、結局Pのn回積を取らなきゃいけないわけ？無理じゃない？」

という話になると思います。しかし、実はある条件の下ではnを十分大きく取ると、この $P^n$ の各要素はある値に収束し、簡単にその値を計算することが出来ます。今回はその収束について確認しようと思います。

カエルの例再び

石1,石2があって、どちらかの石の上にカエルが乗っています。そして、1秒後に
・石1にいて石2に乗り移る確率が50%
・石1にいてそのまま石1に居続ける確率が50%
・石2にいて石1に移る確率を80％
・石2にいてそのまま石2に居続ける確率が20％
であるとします。この時推移確率行列 $P$ は次のようになるということは前回やりました。

$P=\left( \begin{array}{ccc} 0.5 & 0.5 \\ 0.8 & 0.2 \\ \end{array} \right)$

そしてチャップマンコルモゴロフ方程式から、n秒後の推移確率行列は $P^n$ でした。

計算の方法とエルゴード性

で、 $P^n$ はどうやって出すんだという話に入ります。
行列の対角化を行うためにまず $P$ の固有値を導きます。固有値 $λ$ は次の方程式を満たすので、これを解く。

$det(P-λI_2)=0$
ただし、 $I_2$ とは2行2列単位行列を表します。 $det()$ は行列式です。

解くと $λ=1,-0.3$ が得られます。この固有値を使って次のような行列 $Λ$ を作ります。

$Λ=\left( \begin{array}{ccc} 1 & 0 \\ 0 & -0.3 \\ \end{array} \right)$

固有方程式から
$PM=MΛ$ を満たす行列Mが存在し、これを求めてやると、

$M=\left( \begin{array}{ccc} 1 & -0.5 \\ 1 & 0.8 \\ \end{array} \right)$

さらに、Mの逆行列 $M^{-1}$ は、次のようになるので、

$M^{-1}=\frac{1}{1.3}\left( \begin{array}{ccc} 0.8 & 0.5 \\ -1 & 1 \\ \end{array} \right)$

これを $PM=MΛ$ の両辺に後ろから掛けてやると、

$P=MΛM^{-1}$

が得られます。ここで $MM^{-1}$ に注意すると、 $P^n$ は、

$P^n=MΛ^nM^{-1}$

つまり、

$P^n=\frac{1}{1.3}\left( \begin{array}{ccc} 1 & -0.5 \\ 1 & 0.8 \\ \end{array} \right)\left( \begin{array}{ccc} 1^n & 0 \\ 0 & (-0.3)^n \\ \end{array} \right)\left( \begin{array}{ccc} 0.8 & 0.5 \\ -1 & 1 \\ \end{array} \right)$

nを十分大きく取れば、 $(0.3)^n$ なんぞほとんど0に近くなるので、真ん中の行列は1行1列目が1で他が0の行列になります。つまり、次のようになります。

$P^n=\frac{1}{1.3}\left( \begin{array}{ccc} 0.8 & 0.5 \\ 0.8 & 0.5 \\ \end{array} \right)$

なんと、初期値(一番最初にカエルがどこにいたか)に関係なく、石1にいる確率は $\frac{0.8}{1.3}$ だし、石2にいる確率は $\frac{0.5}{1.3}$ になりました。

このnを大きくしていくと初期値に依存しなくなる性質をエルゴード性と呼びます。

シミュレーション

本当に収束するのか、どれくらいで収束するのかRでシミュレーションしてみましょう。

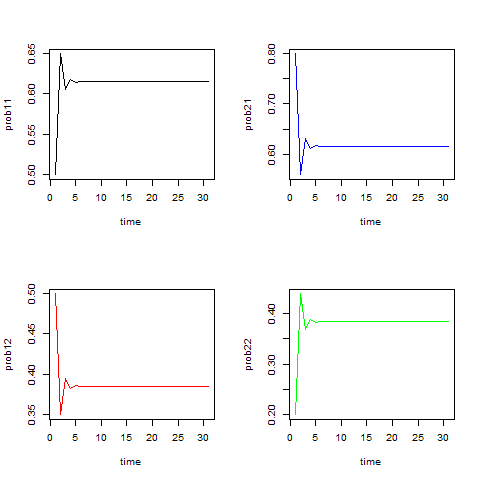
先ほどのカエルの例について、
推移確率行列の各要素を時間を少しずつ増やしてプロットしてみました。4つ全ての要素で値が収束していることが確認できます。

f:id:bananarian:20180827125332p:plain

Rのコードは次の通りです。

time=1:30
P=matrix(c(0.5,0.8,0.5,0.2),2,2)
Pn=matrix(c(0.5,0.8,0.5,0.2),2,2)
prob11=c()
prob12=c()
prob21=c()
prob22=c()
prob11[1]=Pn[1,1]
prob12[1]=Pn[1,2]
prob21[1]=Pn[2,1]
prob22[1]=Pn[2,2]
for(i in time){
	Pn=Pn%*%P
	prob11[i+1]=Pn[1,1]
	prob12[i+1]=Pn[1,2]
	prob21[i+1]=Pn[2,1]
	prob22[i+1]=Pn[2,2]
}
time=c(time,31)
par(mfcol=c(2,2))
plot(time,prob11,type="l")
plot(time,prob12,type="l",col="red")
plot(time,prob21,type="l",col="blue")
plot(time,prob22,type="l",col="green")

まだまだMCMCまでの道のりは遠そうですが、少しずつ記事書いていきます。