線形仮定を置かない相関係数の解釈~共分散に基づくもの~

今まではずっと因果関係の文脈で相関係数の話をしてきましたが、今回は最も仮定を置かない形で、自然な相関係数の解釈って何だろうという話をします。

今まで執拗に、相関係数で因果を見る場合には無意識に「線形の仮定」を置いている。

という話をし、相関係数が高いとは線形関係があることではなく、線形関係を既に仮定した上で、じゃあどの程度関係が強いか見ているにすぎないという話をしてきました。

では、最後に

相関係数の値が高いと必ず線形関係であるとは限らないならば、

線形の仮定を置かずに「相関係数が高い」という事実はどう解釈すればいいのか

と言う話をして終わろうと思います。

一番初めの記事で、相関係数とは次のようなものだと書きました。
$\rho=\frac{Cov[X,Y]}{\sigma_x\sigma_y}$

この時点では、線形の仮定はありませんよね。

つまり、この式自体をそのまま解釈することが相関係数の最も自然な解釈です。

これをそのまま見つめてやると、

共分散を二種類の標準偏差で標準化していると考えることが出来ますね。

共分散とは要はプロットした場合に第一、第三象限にプロットされるか、第二、第四象限にプロットされるかという話をしているにすぎません。要はこういうこと

f:id:bananarian:20181106123451p:plain

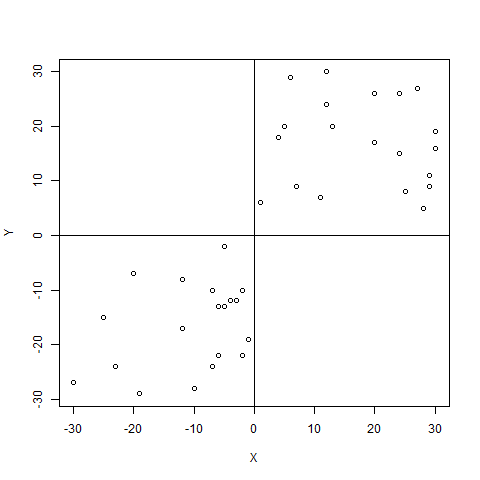
ちなみに↑のデータの相関係数を出してやると0.79あります。

当然、ここに線形仮定は介在しません。

つまり、この時点で相関が高いとはどう解釈すればよいかと言うと

「何かしらの緩い関係はありそうだ」

であって、別に因果関係があるだとか線形関係があるだとか、ましてや正規分布がーなんて話は言えないわけです。

つまり、相関係数を使用する場合、各人使用者は無意識に仮定を置いてからはじめてしまっているわけです。

最も仮定のないピュアな相関係数は「何かしらの関係がある」しか言えないわけで、

そこに因果を考えようとした瞬間、使用者は無意識に線形仮定を加えていて、前回やった最小二乗法に基づいた相関係数を見るわけです。

よって最もピュアな相関係数を考えるにあたって注意すべきは「外れ値があるかどうか」の1点のみなわけです。
※共分散が存在しないといけないため、外れ値の出る分布はまずい

ただ、何度も言っているように、ピュアな相関係数は仮定が無い分解釈しにくい、結局「何かしらの関係がありそう」しか言えないことになるので、せめて線形仮定を置いた相関係数で考えることで、初めて因果の話に繋がるわけです。