【初心者向け】相関係数を動かしてポートフォリオのリスク・リターン曲線を確認してみる

前回は２資産ポートフォリオのリターンの期待値、分散、そしてトータルリスクの導出についてやりました。
詳しくはこちら
bananarian.hatenablog.com

今回はポートフォリオのトータルリスクと期待リターンの関係についてRのプロットを使って確認していこうと思います。

前回の復習

資産a、資産bの2資産に投資を行う際のポートフォリオのリターン $R_p$ は投資比率 $w$ を使って次のように表すことができる。

$R_p=w_aR_a+w_bR_b$

更にその期待値、分散、トータルリスクは次のようになる。

$E [ R_p ]=w_a E [ R_a ]+w_b E [ R_b ]$

$Var [ R_p ]=w_a^2 Var [ R_a ]+w_b^2 Var [ R_b ] + 2w_aw_b cov[ R_a,R_b ]$

$\sigma_p=\sqrt{Var [ R_p ]}$

実際の図をもって確認

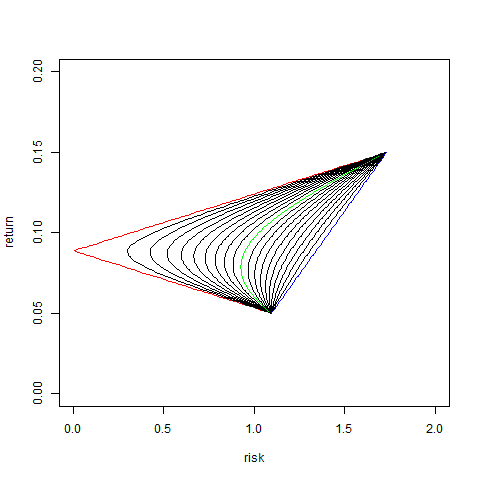
次のような状況でのリスクとリターンの図を描いてみます。

資産1
・期待リターン:0.15
・リターンの分散:3

資産2
・期待リターン:0.05
・リターンの分散:1.2

相関係数の値を-1から1の範囲で変えていく
相関係数が1の時は青色
相関係数が-1の時は赤色
相関係数が0の時は緑色
相関係数がそれ以外の場合は黒色
f:id:bananarian:20180830010237p:plain

コードは次のよう。

#資産1の期待値(ex),分散(var),標準偏差(sd)
sisan1_ex=0.15
sisan1_var=3
sisan1_sd=sqrt(sisan1_var)

#資産2の期待値(ex),分散(var),標準偏差(sd)
sisan2_ex=0.05
sisan2_var=1.2
sisan2_sd=sqrt(sisan2_var)

#投資比率
w1=seq(0,1,0.01)
w2=1-w1

#ポートフォリオの期待値(ex)
port_ex=w1*sisan1_ex+w2*sisan2_ex

png("1.png")
plot(c(0,2),c(0,0.2),type="n",xlab="risk",ylab="return")

#資産1,資産2の相関係数を-1から1の範囲で動かす
for(ro in seq(-1,1,0.1)){
	#ポートフォリオの分散(var)
	port_var=(w1^2)*sisan1_var+(w2^2)*sisan2_var+2*w1*w2*sisan1_sd*sisan2_sd*ro

	if(ro==-1){
		#相関係数が1の時は赤色でプロット
		points(sqrt(port_var),port_ex,type="l",col="red")
	}
	else{
		#相関係数が0の時は緑色でプロット
		if(ro==0){
			points(sqrt(port_var),port_ex,type="l",col="green")
		}
		else{
			#相関係数が1の時は青色でプロット
			if(ro==1){
				points(sqrt(port_var),port_ex,type="l",col="blue")
			}
			else{
				#それ以外は黒でプロット
				points(sqrt(port_var),port_ex,type="l")
			}	
		}
	}
}
dev.off()

さらに、投資比率を1以上、もしくは負の値にすることで、資金の借り入れ、空売りを表現することが出来、よりリスクは高いが期待リターンの大きい投資が可能になる。それをプロットすると次のようになる。
f:id:bananarian:20180830010641p:plain

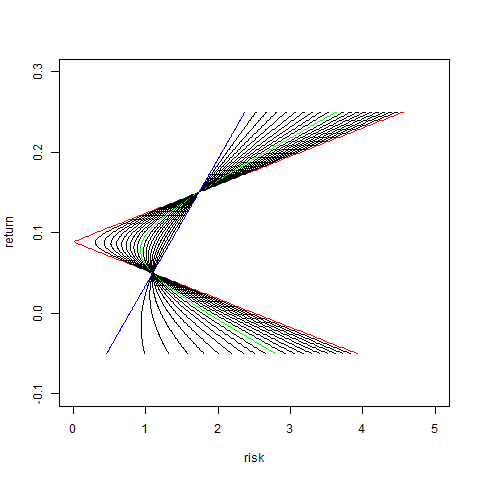
#変更点
w1=seq(-1,2,0.01)
plot(c(0,5),c(-0.1,0.3),type="n",xlab="risk",ylab="return")

実際は相関係数が定まる代わりに、投資対象が増大するわけですが、このようなリスクリターン平面を描くことでポートフォリオのリスクとリターンの関係を確認することが出来ます。

また、図を見ると確認できますが、正の相関をしている資産の組ではリスク分散効果がなく、分散投資をしたところであまり意味はなさそうです。一方、負の相関をしている組では、リスク0のポートフォリオが存在しています。