Rで行える線形回帰分析法の一覧とその方法~最小二乗法・最尤法・ベイズ~

今回は、線形回帰分析に関するRでの分析法を1記事にまとめておこうと思います。

線形回帰分析とは
シミュレーション用データ
最小二乗法
最尤法
ベイズ
３つの手法の比較
- 注意

線形回帰分析とは

今更感がありますが、一応線形回帰分析の説明をしておきます。
被説明変数(予測変数) $Y_i$ が説明変数 $X_{i,k}$ によって、次のような構造になっていると仮定します。

$Y_i =\alpha_0+\alpha_1 X_{i,1}+...+\alpha_K X_{i,K}+\epsilon_i$

ただし、
$\alpha_0,...\alpha_K$ は未知パラメータ
$\epsilon_i$ は誤差項(よってこれは確率変数)
$\epsilon_i$ は各々独立にある確率分布に従っているとする。
$Var[\epsilon_i]=\sigma^2$

この時、 $Y_i$ の条件付き分布 $Prob(Y_i|\alpha,\sigma,X)$ を考えておく。

この時の未知パラメータの推定量として妥当なものを様々な手法から検討したいというわけです。

シミュレーション用データ

適当に被説明変数 $Y$ と説明変数行列 $X$ を用意しておくことにします。

X1=sample(1:100,60,replace=FALSE)
X2=sample(30:50,60,replace=TRUE)
y=10+0.4*X1+5.2*X2+rnorm(60,0,sqrt(3))

サンプルサイズ $60$ ,誤差の分散が $\sqrt{3}=1.73$ のデータを使います。

最小二乗法

計算

最小二乗法は次のように計算します。
$Y=(Y_1,...Y_n)'$
$X=\begin{pmatrix} 1&X_{1,1}&\cdots&X_{1,K} \\ \vdots&\vdots&\ddots&\vdots \\ 1&X_{n,1}&\cdots&X_{n,K} \\ \end{pmatrix}$
$\alpha =(\alpha_0,\cdots,\alpha_K)'$
$\epsilon = (\epsilon_1,\cdots,\epsilon_n)'$

$Y=X \alpha +\epsilon$

といった形で行列表記すると、誤差は次のように表せます。
$\epsilon=Y-X \alpha$

よって誤差の二乗和は次のように表せます。
$\epsilon'\epsilon=(Y-X \alpha)'(Y-X \alpha)$

この誤差の二乗和を最小にするような $\alpha$ の値 $\hat{\alpha}$ を求めます。

$\epsilon'\epsilon=(Y-X \alpha)'(Y-X \alpha)=Y'Y-2Y'X \alpha+\alpha'X'X\alpha$
$\frac{\partial}{\partial \alpha}\epsilon'\epsilon=-2X'Y+2(X'X)\alpha$
$\hat{\alpha}=(X'X)^{-1}X'Y$

また、 $\sigma^2$ の不偏推定量 $\hat{\sigma}^2$ は
$\hat{\sigma}^2=\frac{(Y-X \hat{\alpha})'(Y-X \hat{\alpha})}{n-K}$

Rによる最小二乗法

Rで最小二乗推定値を求めるには、lm関数を利用します。

model1=lm(y~X1+X2)
n=length(y)
k=3
#係数の推定値を取り出す
a_hat1=coef(model1)
X=cbind(1,X1,X2)
#sigmaを計算する
sigma_hat1=t(y-X%*%a_hat1)%*%(y-X%*%a_hat1)/(n-k)

出力

> a_hat1
(Intercept)          X1          X2 
 10.2205439   0.4014095   5.1984349 
> sqrt(sigma_hat1)
         [,1]
[1,] 1.706484

実際の $\alpha,\sigma$ は
$\alpha_0=10,\alpha_1=0.4,\alpha_2=5.2,\sigma=1.73$
なので、そこそこ近い値が出ていることが分かります。

最小二乗法の特徴

・最小二乗法を使った推定量は、不偏性、一致性がある。更に、最良線形不偏推定量としても機能する。
・分布を仮定することなく、推定できる。

最尤法

計算

$\epsilon_i$ が正規分布に従っていると仮定します。
ここで、 $Prob(Y|\alpha,X,\sigma)$ は次のよう。

$Prob(Y|\alpha,X,\sigma)=(\frac{1}{\sqrt{2 \pi \sigma^2}})^n exp(-\sum_{i=1}^n \frac{(Y_i-X_{\{i,\}}\alpha)^2}{2\sigma^2})$

最尤法では対数尤度 $ln(Y;\alpha,X,\sigma)$ を取ると計算しやすいです。
$ln(Y;\alpha,X,\sigma)=log(Prob(Y|\alpha,X,\sigma))$
$=-nlog(2 \pi)-2nlog(\sigma)-\sum_{i=1}^n \frac{(Y_i-X_{\{i,\}}\alpha)^2}{2\sigma^2}$
$=-nlog(2 \pi)-2nlog(\sigma)-\frac{(Y-X \alpha)'(Y-X \alpha)}{2\sigma^2}$

対数尤度を最大化する $\alpha$ の値 $\hat{\alpha}_{ML}$ と $\sigma$ の値 $\hat{\sigma}_{ML}$ を求めたい。

$\frac{\partial}{\partial \alpha}ln(Y;\alpha,X,\sigma)=0$
$\frac{\partial}{\partial \sigma^2}ln(Y;\alpha,X,\sigma)=0$

を満たす値を求めればよく、計算してやると
$\hat{\alpha}_{ML} =\hat{\alpha} =(X'X)^{-1}X'Y$
$\hat{\sigma}_{ML}^2=\frac{(Y-X \hat{\alpha}_{ML})'(Y-X \hat{\alpha}_{ML})}{n}$

Rによる最尤推定

先ほどの計算式を打ち込んでみます。

a_hat=solve(t(X)%*%X)%*%t(X)%*%y
sigma_hat2=(t((y-X%*%a_hat))%*%(y-X%*%a_hat))/n

出力

> a_hat
         [,1]
   10.2205439
  0.4014095
  5.1984349
> sqrt(sigma_hat2)
         [,1]
[1,] 1.663275

係数の推定値は最小二乗法と同じですが、誤差の標準偏差の推定値が異なりますね。

最尤法の特徴

・最尤推定量は一致性を持つ
・漸近的に有効かつ不偏性を持つ
・分布を仮定する必要がある
・汎用性が高い

ベイズ

解説

ベイズではパラメータの事後分布 $P(\alpha_k|X,y),P(\sigma|X,y)$ を求めるか、その事後分布からのサンプリングを行うことでパラメータの分布を考えます。その際、推定値として何を採用するかが問題となってきます。事後平均、事後の中央値、最頻値等色々考えられます。
事前分布の選択も重要です。

Rstanによる実装(非ベクトル化編)

Stanによるモデリングを行います。
まず、普通にベクトル化せずに書いてみます。
Stanではパラメータに対して分布を設定しておかなかった場合、勝手に無情報事前分布が割り当てられます。

#パッケージ
library(rstan)
#モデル
model2="
data{
	int N;
	int K;
	real X[N,(K-1)];
	real Y[N];
}

parameters{
	real a[K];
	real<lower=0> sigma;
}

transformed parameters{
	real mu[N];
	for(n in 1:N){
		mu[n]=a[1];
		for(k in 2:K){
			mu[n]=mu[n]+a[k]*X[n,(k-1)];
		}
	}
}

model{
	for(n in 1:N){
		Y[n] ~ normal(mu[n],sigma);
	}
}
"
data_list=list(N=n,K=k,X=cbind(X1,X2),Y=y)
fit=stan(model_code=model2,data=data_list,seed=1234)

出力

> fit
Inference for Stan model: c126dea47c42ac03e7ce323de93ea362.
4 chains, each with iter=2000; warmup=1000; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=4000.

         mean se_mean   sd   2.5%    25%    50%    75%  97.5% n_eff Rhat
a[1]    10.26    0.04 1.66   6.95   9.17  10.28  11.40  13.47  1487    1
a[2]     0.40    0.00 0.01   0.38   0.40   0.40   0.41   0.42  2709    1
a[3]     5.20    0.00 0.04   5.12   5.17   5.20   5.22   5.28  1502    1
sigma    1.74    0.00 0.17   1.45   1.62   1.73   1.85   2.11  2438    1

今回は事後平均を推定値として採用するとします。
この場合推定値は $\hat{a_0}_{Bayes}=10.26,\hat{a_1}_{Bayes}=0.40,\hat{a_2}_{Bayes}=5.20,\hat{\sigma}_{Bayes}=1.74$

より効率の良いコード(ベクトル化編)

Stanはベクトル化した方が計算速度が速くなることがあります。
ベクトル化したコードをもう一度書いてみます。

model3="
data{
	int N;
	int K;
	matrix[N,K] X;
	vector[N] Y; 
}

parameters{
	vector[K] a;
	real<lower=0> sigma;
}

transformed parameters{
	vector[N] mu;
	mu = X*a;
}

model{
	Y~normal(mu,sigma);
}
"

data_list2=list(N=n,K=k,X=X,Y=y)
fit2=stan(model_code=model3,data=data_list2,seed=1234)

計算速度を調べるためにはproc.time関数を使います。

t=proc.time()
fit=stan(model_code=model2,data=data_list,seed=1234)
proc.time()-t

t=proc.time()
fit2=stan(model_code=model3,data=data_list2,seed=1234)
proc.time()-t

model2の出力

> proc.time()-t
   ユーザ   システム       経過  
      3.92       0.56       4.59

model3の出力

> proc.time()-t
   ユーザ   システム       経過  
      3.55       0.17       3.80

経過時間がmodel3の方が早くなっていることが確認出来ます。

ベイズの特徴

・最尤法の一般化概念と捉えることも出来る
・最尤法との違いは、最尤法はmonotonicな変数変換に対して不変なのに対して、ベイズは事後平均等を用いるため変化してしまう
・階層モデル等に拡張することも出来る
・事後の条件付き分布を見ているにすぎないことに注意

３つの手法の比較

実際は背後の真のパラメータの値によりけりなので、それぞれの特徴を考慮した上で方法を選ぶことになるわけですが、今回はシミュレーション出来るので、サンプルサイズを変えて比較してみました。

N=10:300
a0=10
a1=0.4
a2=5.2
sigma=sqrt(3)
a0hat1=c()
a1hat1=c()
a2hat1=c()
a0hatB=c()
a1hatB=c()
a2hatB=c()
sigmahat1=c()
sigmahat2=c()
sigmahatB=c()

for(nn in N){
	X1=sample(1:1000,nn,replace=FALSE)
	X2=sample(300:500,nn,replace=TRUE)
	y=a0+a1*X1+a2*X2+rnorm(nn,0,sigma)
	model1=lm(y~X1+X2)
	n=length(y)
	k=3
	X=cbind(1,X1,X2)
	a0hat1[which(N==nn)]=coef(model1)[1]
	a1hat1[which(N==nn)]=coef(model1)[2]
	a2hat1[which(N==nn)]=coef(model1)[3]
	sigmahat1[which(N==nn)]=sqrt(t(y-X%*%a_hat1)%*%(y-X%*%a_hat1)/(nn-k))
	sigmahat2[which(N==nn)]=sqrt(t(y-X%*%a_hat1)%*%(y-X%*%a_hat1)/nn)
	data_list2=list(N=n,K=k,X=X,Y=y)
	fit2=stan(model_code=model3,data=data_list2,seed=1234,chains=1)
	sigmahatB[which(N==nn)]=mean(rstan::extract(fit2)$sigma)
	a0hatB[which(N==nn)]=mean((rstan::extract(fit2)$a)[,1])
	a1hatB[which(N==nn)]=mean((rstan::extract(fit2)$a)[,2])
	a2hatB[which(N==nn)]=mean((rstan::extract(fit2)$a)[,3])
}

par(mfcol=c(2,2))	
plot(N,a0hat1,xlab="sample size",ylab="",main="a0",col="red",type="l")
points(N,rep(a0,length(N)),col="black",type="l")
points(N,a0hatB,col="green",type="l")
legend("topright", legend = c("OLS","Bayes"), col = c("red","green"),lty=c("solid","solid"))

plot(N,a1hat1,xlab="sample size",ylab="",main="a1",col="red",type="l")
points(N,rep(a1,length(N)),col="black",type="l")
points(N,a1hatB,col="green",type="l")
legend("topright", legend = c("OLS","Bayes"), col = c("red","green"),lty=c("solid","solid"))

plot(N,a2hat1,xlab="sample size",ylab="",main="a2",col="red",type="l")
points(N,rep(a2,length(N)),col="black",type="l")
points(N,a2hatB,col="green",type="l")
legend("topright", legend = c("OLS","Bayes"), col = c("red","green"),lty=c("solid","solid"))

plot(N,sigmahat1,xlab="sample size",ylab="",main="sigma",col="red",type="l")
points(N,rep(sigma,length(N)),col="black",type="l")
points(N,sigmahatB,col="green",type="l")
points(N,sigmahat2,col="yellow",type="l")
legend("topright", legend = c("OLS","Bayes","MLE"), col = c("red","green","yellow"),lty=c("solid","solid","solid"))

出力はこんな感じ。
f:id:bananarian:20190111002223p:plain
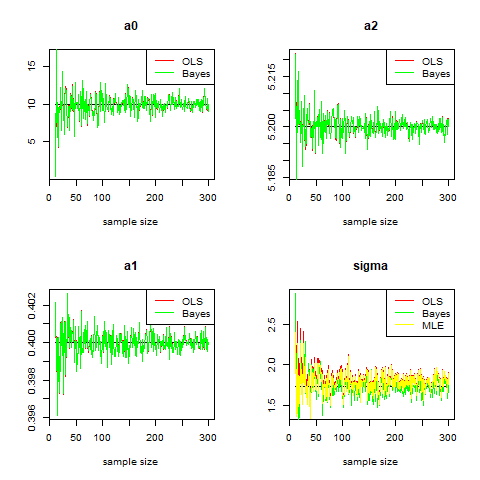
$\sigma$ の推定値が推定方法によって収束スピードが異なっている様子が見て取れます。

試しにもう少し比較してみると

par(mfcol=c(2,2))
plot(N,sigmahat1,xlab="sample size",ylab="",main="sigmaOLS",col="red",type="l",ylim=c(1,3))
points(N,rep(sigma,length(N)),col="black",type="l")
plot(N,sigmahat2,xlab="sample size",ylab="",main="sigmaMLE",col="red",type="l",ylim=c(1,3))
points(N,rep(sigma,length(N)),col="black",type="l")
plot(N,sigmahatB,xlab="sample size",ylab="",main="sigmaBayes",col="red",type="l",ylim=c(1,3))
points(N,rep(sigma,length(N)),col="black",type="l")

f:id:bananarian:20190111003111p:plain

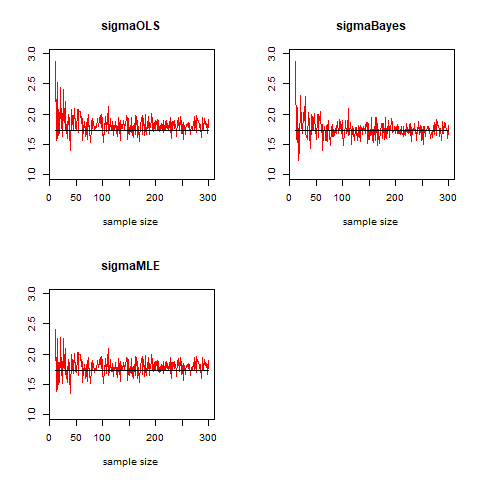
プロットをした印象としては、ある程度サンプルサイズの大きくなると、事後分布からの事後平均を使ったものが安定していそうな気がします。
真の値との誤差も求めてみます。

今回求めた全ての推定値から誤差を求めた場合

> sum((sigmahat1-sigma)^2)
[1] 9.220136
> sum((sigmahat2-sigma)^2)
[1] 6.285238
> sum((sigmahatB-sigma)^2)
[1] 6.807877

最尤推定量を使った値が最も誤差の総和が小さい

一方、サンプルサイズが50より大きい所で見た場合

> sum((sigmahat1[40:length(N)]-sigma)^2)
[1] 4.474911
> sum((sigmahat2[40:length(N)]-sigma)^2)
[1] 3.742564
> sum((sigmahatB[40:length(N)]-sigma)^2)
[1] 3.059328