Rで試すマルコフ連鎖 - バナナでもわかる話

前回はマルコフ連鎖を極力数式を使わず、イメージ出来るよう説明しました。

bananarian.hatenablog.com

今回は、よりマルコフ連鎖についてイメージを持てるようRを使ってシミュレーションをしてみました。Rのコードも記載していきます。

数学的な理解

まず、前回のおさらいですが、マルコフ連鎖とは一つ前の状態だけが次の状態の決定要因になっているような時系列のことを指すと説明しました。今回はもう少し数学的な表記で書くことにします。

$(E,ε)$ を可測空間とする。これをマルコフ連鎖が動く空間であるとし、この時この空間をマルコフ連鎖の状態空間と呼ぶ。

いきなり難しいことを言い出してなんだという方にちょっと例を出しておきます。
例えば前回の記事(【初心者向け】雰囲気で理解するマルコフ連鎖 - バナナでもわかる話)で出したカエルの例であれば、
カエルは石1,石2を交互にいったりきたりしていたわけなので、カエルの状態は「石1にいる」か「石2にいる」かしかありません。
この時の状態空間 $(E,ε)$ の $E$ は $E=(1,2)$ となります。

要は $E$ は起こりうる状態を全て書きつくしたものと考えてください。

更に $(Ω,F,P)$ を確率空間とし、その確率空間上の確率変数列{ $X_n$ }について任意のn(nは整数)、 $i_0,i_1,...i_{n+1}\in E$ に対して $P(X_{n+1}=i_{n+1}|X_0=i_0,....X_n=i_n)=P(X_{n+1}=i_{n+1}|X_n=i_n)$ となるとき、マルコフ連鎖であるという。

要は一つ前の状態以外は関係ないよーということと、今から扱うものは確率的な動きをするよーということを数学的に書き表したものです。

マルコフ連鎖の具体例

ランダムウォーク

まず、ランダムウォークというものがあります。これは例えば次のような動きを指します。
$確率0.5で X_{n+1}=X_n+1$
$確率0.5で X_{n+1}=X_n-1$
となるような列を考える。これをシミュレーションしてみると次のようになります。
f:id:bananarian:20180826143732p:plain

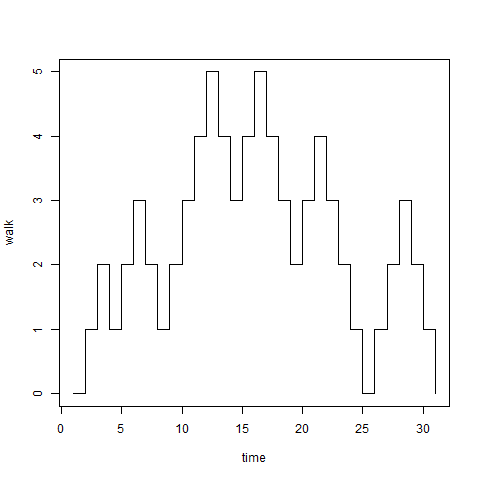
初期値 $X_0=0$ としておいて、そこから等確率で1個上に上がるか1個下に下がるか決まります。

これは例えば2のところにいたとすると次は1か3にしか行かないのでマルコフ連鎖です。

このシミュレーションのRコードは次のよう。

init=0
time=1:30
walk=c()
walk[1]=init
for(i in time){
	if(rbinom(1,1,0.5)==1){
		init=init+1
	}	
	else{
		init=init-1
	}
walk[i+1]=init
}
time=c(time,length(time)+1)
plot(time,walk,type="s")

この時の $E$ は $E=(整数全体)$ となります。

ちなみに、もっとたくさん出してやるとこんな風になります。細かくしてやると株価の動きみたいに見えなくもないですね。
f:id:bananarian:20180826144520p:plain

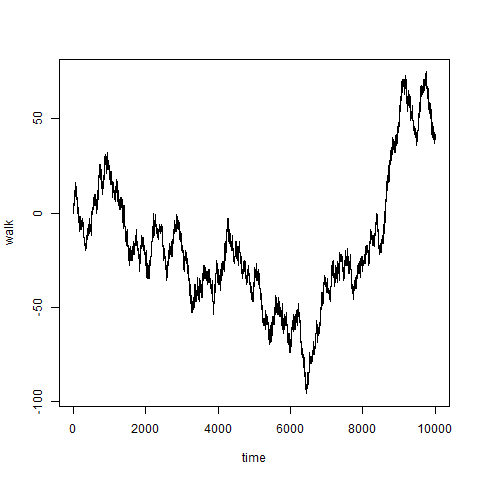
init=0
time=1:10000
walk=c()
walk[1]=init
for(i in time){
	if(rbinom(1,1,0.5)==1){
		init=init+1
	}	
	else{
		init=init-1
	}
walk[i+1]=init
}
time=c(time,length(time)+1)
plot(time,walk,type="s")

二次元ランダムウォーク

二次元空間を先ほどと同じような方法でランダムに動かすこともできて、これもマルコフ連鎖です。数式で表現するなら次のようになります。

座標を $(X_i,Y_i)$ とする。
$確率0.5で X_{n+1}=X_n+1$
$確率0.5で X_{n+1}=X_n-1$
$確率0.5で Y_{n+1}=Y_n+1$
$確率0.5で Y_{n+1}=Y_n-1$
と動くランダムウォークを考える。
これをシミュレーションすると次のようになります。
f:id:bananarian:20180826145007p:plain

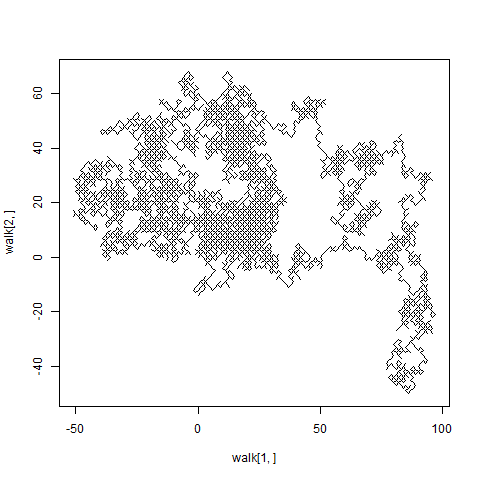
コードは次のとおり

#二次元ランダムウォーク
init1=0
init2=0
time=1:10000
walk=matrix(,2,length(time)+1)
walk[1,1]=init1
walk[2,1]=init2
for(i in time){
	if(rbinom(1,1,0.5)==1){
		init1=init1+1
	}	
	else{
		init1=init1-1
	}
	if(rbinom(1,1,0.5)==1){
		init2=init2+1
	}	
	else{
		init2=init2-1
	}
walk[1,i+1]=init1
walk[2,i+1]=init2
}
plot(walk[1,],walk[2,],type="l")

自己回帰過程

$X_{n+1}=αX_n+ν_{n+1}$
$ただし、ν_iは確率変数$
のように前の状態と関係しているんだけども、適当な誤差が混ざって来るような時系列を自己回帰過程と呼びます。

これもシミュレーションしてみます。
今回はα=0.3,νは正規分布に従うものとして試してみました。
f:id:bananarian:20180826145615p:plain

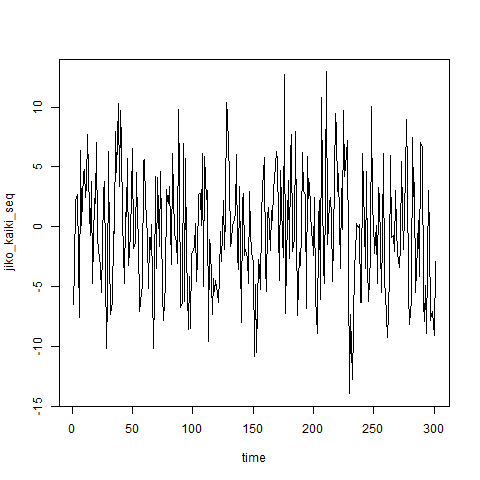
コードは次の通りです。

#自己回帰過程
init=rnorm(1,0,10)
jiko_kaiki_seq=c()
time=1:300
jiko_kaiki_seq[1]=init
for(i in time){
	X=jiko_kaiki_seq[i]
	y=0.3*X+rnorm(1,0,5)
	jiko_kaiki_seq[i+1]=y
}
time=c(time,length(time)+1)
plot(time,jiko_kaiki_seq,type="l")

ARCHモデル

分散が不均一な時系列データ、要はなんかわかりにくくバラついているデータに対して当てはめるモデルとしてARCHモデルというものがあります。これには例えば次のようなものがあり、これはマルコフ連鎖になります。
$X_{n+1}=(\sqrt{0.2+0.3{X_n}^2} )ν_{n+1}$

シミュレーションしてみるとこんな感じ。
f:id:bananarian:20180826150542p:plain

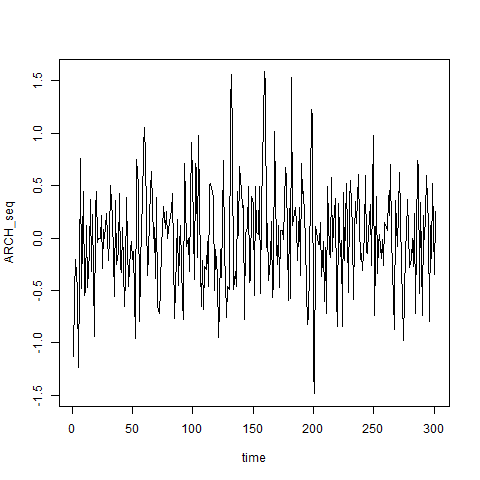
#ARCHモデル(ドリフト条件を満たす)
init=rnorm(1,0,10)
ARCH_seq=c()
time=1:300
ARCH_seq[1]=init
for(i in time){
	X=ARCH_seq[i]
	y=sqrt((0.2+0.3*X^2))*rnorm(1,0,1)
	ARCH_seq[i+1]=y
}
time=c(time,length(time)+1)
plot(time,ARCH_seq,type="l")

ちなみにいつか別の記事で説明しますが、ドリフト条件という条件があって、それを満たさないARCHモデルは少し暴れます。シミュレーションすると次のようになります。
f:id:bananarian:20180826150905p:plain

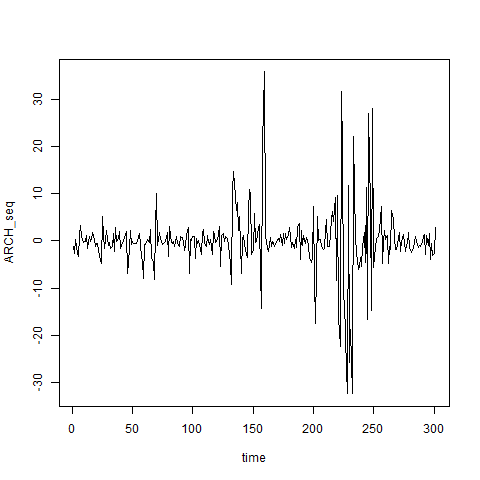
#ARCHモデル(ドリフト条件を満たさない)
init=rnorm(1,0,10)
ARCH_seq=c()
time=1:300
ARCH_seq[1]=init
for(i in time){
	X=ARCH_seq[i]
	y=sqrt((1.2+1.5*X^2))*rnorm(1,0,1)
	ARCH_seq[i+1]=y
}
time=c(time,length(time)+1)
plot(time,ARCH_seq,type="l")

以上マルコフ連鎖の具体例でした。