2019-01-18

多項プロビットモデルだけで1冊書いてる本を見つけた

今日大学の図書館の書庫を彷徨っていたら、面白そうな本を見つけました。

Multinomial Probit: The Theory and Its Application to Demand Forecasting
<br />

なんとこの本、multinomial probit(多項プロビットモデル)だけで1冊の本になっているらしく、多項プロビット関連の話でそんなに書くことあるのだろうか....と思いつつ興味本位で借りてみました。

一応目次だけ書いておくと
chapter1 An introduction to Disaggregate Demand Modeling in the Transportation Field
chapter2 Maximum-Likelihood Estimation: Computational Aspects
chapter3 Statistical Aspects of Multinomial Probit Model Calibration
chapter4 Prediction: Mechanical Aspects
chapter5 The Statistical Interpretation of Predictions
Appendix A~D

という構成。

とりあえず、一通り読んだらまた追加でレビューでも書こうと思います。

2019-01-17

Rで行えるプロビット回帰に関するまとめ~最尤法、ベイズ~

R Stan ベイズ統計学統計

今回はRでプロビット回帰を行う際に使用できる分析方法と、その注意点を上げておきます。

プロビット回帰とは
最尤法
ベイズ
注意点とコメント
関連記事

プロビット回帰とは

予測変数が0か1しかないとき、例えば倒産する(1)、倒産しない(0)や、購買する(1)、購買しない(0)等のケースでは、普通線形回帰分析は利用しません。まあ別に利用することも出来るけど、予測値に1以上の値や0未満の値が出て来てどう考えたら良いかわからなくなるからです。
そこで、ロジスティック回帰やプロビット回帰といったような手法を利用します。

最尤法

モデル

プロビットモデルは次のようなモデルです。
まず、1が出る確率 $P(Y_i=1|X)$ を次のように定義します。

$P(Y_i=1|X) =\int_{-\infty}^{\alpha+\beta X} \frac{1}{\sqrt{2 \pi}} exp(-\frac{z^2}{2}) dz$

要は正規分布の分布関数です。分布関数であれば値は $[0,1]$ の範囲に収まるので、これを利用します。

後は $P(Y_i|X)$ の $i=1,2,\cdots,n$ に関する同時分布を考えて、それを尤度とします。
解は解析的には得られないので、数値最適化を利用することになります。

Rによるコード

Rでは、基本パッケージにプロビット回帰を行う関数が用意されており、簡単に行うことが出来ます。

glm(y~X1+X2+X3,family=binomial(probit))

シミュレーション

それでは、サンプルサイズを500から100000まで動かして、係数比を見てやることにします。

n_max=100000
nseq=seq(500,n_max,500)
glmbeta1_seq=c()
glmbeta2_seq=c()
glmbeta3_seq=c()
glmbeta4_seq=c()
beta0=-0.5
beta1=0.3
beta2=0.5
beta3=0.5
X1=sample((-50):50,n_max,replace=TRUE)
X2=sample(50:70,n_max,replace=TRUE)
X3=sample((-70):(-50),n_max,replace=TRUE)
mu=beta0+beta1*X1+beta2*X2+beta3*X3
probabl=pnorm(mu)
y=c()
for(p in probabl){
	if(p>=runif(1)){
		y[which(probabl==p)]=1
	}
	else{
		y[which(probabl==p)]=0
	}
}


for(i in nseq){
	res=glm(y[1:i]~X1[1:i]+X2[1:i]+X3[1:i],family=binomial(probit))
	glmbeta1_seq[which(nseq==i)]=coef(res)[1]
	glmbeta2_seq[which(nseq==i)]=coef(res)[2]
	glmbeta3_seq[which(nseq==i)]=coef(res)[3]
	glmbeta4_seq[which(nseq==i)]=coef(res)[4]
}

f:id:bananarian:20190117113303p:plain
赤線が真の値です。
結構近い値が出力されています。

ただ、ロジスティック回帰もそうですが、サンプルサイズがそこそこ大きくならないと使えない感じがありますね。
特にプロビット回帰だと正規分布の裾がロジットよりも薄いので尚更です。

ベイズ

当然ベイズでも出来ます。Stanを使えばそれ用のコードがあるので結構簡単です。

model="
data{
	int<lower=1> N;
	int<lower=1> K;
	matrix[N,(K-1)] X;
	int<lower=0,upper=1> Y[N];
	
}

parameters{
	vector[K] beta;
}

transformed parameters{
	vector[N] mu;
	for(n in 1:N){
		mu[n]=beta[1];
		for(k in 2:K){
			mu[n] = mu[n]+beta[k]*X[n,(k-1)];
		}
	}
}

model{
	Y ~bernoulli(Phi(mu));
}
"


data=list(N=length(y),K=4,X=cbind(X1,X2,X3),Y=y)
fit=stan(model_code=model,data=data,seed=1234,pars="beta",chains=1)

結果

> fit
Inference for Stan model: c368d88db0144dcae18220ad714858ba.
1 chains, each with iter=2000; warmup=1000; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=1000.

            mean se_mean   sd     2.5%      25%      50%      75%    97.5%
beta[1]    -2.18    0.02 0.25    -2.64    -2.36    -2.19    -2.01    -1.68
beta[2]     0.56    0.00 0.01     0.54     0.55     0.56     0.56     0.57
beta[3]     0.93    0.00 0.01     0.90     0.92     0.93     0.94     0.95
beta[4]     0.92    0.00 0.01     0.88     0.91     0.92     0.92     0.94
lp__    -3218.43    0.09 1.43 -3222.04 -3219.18 -3218.06 -3217.44 -3216.77
        n_eff Rhat
beta[1]   260    1
beta[2]   151    1
beta[3]   154    1
beta[4]   151    1
lp__      260    1

Samples were drawn using NUTS(diag_e) at Thu Jan 17 14:59:04 2019.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

比をとってやると、真の値の比とほぼ同じ値をとっていることがわかります。

> 0.3/0.5
[1] 0.6
> 0.56/0.93
[1] 0.6021505
> 0.56/0.92
[1] 0.6086957

注意点とコメント

・プロビット回帰はロジット回帰よりも分布の裾が軽いので、0か1がまれにしか出ないようなデータには当てはまりが悪くなります。
・多変量に拡張しない限りは、正直ロジットとプロビットの差は裾の部分にしかないので、単なる二項選択ならロジットを使うのがラクチンではある。
詳しくはこちら
人間の選択をモデル化するプロビット・ロジットモデルの違いと経済学的解釈法 - バナナでもわかる話

人間の選択をモデル化するプロビット・ロジットモデルの違いと経済学的解釈法 - バナナでもわかる話
 Rで行えるロジスティック回帰に関するまとめ~最尤法、Penalized Likelihood (Firth)、ベイズ~ - バナナでもわかる話

2019-01-15

Rで行うEMアルゴリズム~ゼロ過剰ポワソン分布を例にして~

ゼロ過剰ポアソン分布 R 統計

今回は、EMアルゴリズムを用いて、ゼロ過剰ポワソン分布のパラメータの推定を行ってみようと思います。

過去記事
最尤推定
EMアルゴリズム
- アルゴリズム
- 実例

過去記事

ゼロ過剰ポワソン分布に関する詳しい説明はこちらをご覧ください。
ゼロ過剰ポアソン分布とは何か - バナナでもわかる話

前にゼロ過剰ポワソン分布に関する尤度の説明は記事にしましたが、今回は潜在変数を利用するので、また新しく説明しようと思います！
ゼロ過剰ポアソン分布の尤度関数 - バナナでもわかる話

最尤推定

ゼロ過剰ポワソン分布の尤度関数

ゼロ過剰ポワソン分布から得られたデータがn個あるとします。
ここで、普通のポワソン分布から出ている(観測されない未知の)サンプルサイズをMと置くことにします。
つまり、ゼロのみからなる標本空間から得られたサンプルがn-M個あると考えても問題ありません。

更に、今回は確率 $\omega$ でゼロのみからなる標本空間からサンプリングされると仮定します。
そうするとこの時の尤度関数 $l(\lambda,\omega)$ は次のようになりますね。ただ、Mは一旦固定しておきます。

$l(\lambda,\omega)= \omega^{n-M} \prod_{i=1}^M \{\frac{(1-\omega) \lambda^{y_i}exp(-\lambda)}{y_i !} \}$

最尤推定量

対数尤度 $ln(\lambda,\omega)$ を求めます。
$ln(\lambda,\omega)=(n-M)log(\omega) +M log(1-\omega)+\sum_{i=1}^M \{y_i log(\lambda)-\lambda -log(y_i !)\}$

Mはとりあえず放っておいて、最尤推定量を求めてみます。
$\frac{\partial ln(\lambda,\omega)}{\partial \omega} =\frac{n-M}{\omega}-\frac{M}{1-\omega}=0$
$\hat{\omega} = 1-\frac{M}{n}$

$\frac{\partial ln(\lambda,\omega)}{\partial \lambda} =-M+\frac{\sum_{i=1}^M y_i}{\lambda}=0$
$\hat{\lambda} = \frac{\sum_{i=1}^M y_i}{M}$

Mの理論値

とりあえず、1以上の値は全て普通のポワソン分布から出ていることがわかっています。そこで1以上の個数 $m=\#(Y_i≧1)$ と置くことにします。
この時点でM≧mであることが分かっています。
さて、何個の0が普通のポワソン分布に属しているかという話ですが、理論的にはポワソン分布から0が出る確率は $exp(-\lambda)$ なので、
サンプルサイズMのもとでの、0の個数に関する期待値は $M exp(-\lambda)$ ですね。そこで、Mの理論値は次のように書けます。

$M = m +M exp(-\lambda)$

Mの理論値にMを使ってることに少し違和感がありますが、これをMについて解いてやります。
$\hat{M}=\frac{m}{1-exp(-\lambda)}$

EMアルゴリズム

$M$ の推定には $\lambda$ を使うし、 $\lambda$ や $\omega$ の推定には $M$ を使います。よって、どちらかが分からない限り推定値を得ることができません。
そこで、EMアルゴリズムという手法を利用します。

EMアルゴリズムでは、 $M$ 又は $\lambda$ に初期値を与えてもう片方を推定し、その推定結果を利用して、またもう片方を推定する...という手順を繰り返し、逐次的に解を得ます。

アルゴリズム

今回は、まず初期値として $\lambda_{init} =\frac{\sum_{i=1}^n y_i}{n}$ を与えることにします。
そして、この $\lambda_{init}$ を利用して $M$ の初期値 $M_1$ を次のように得ます。
$M_1 = \frac{m}{1-exp(-\lambda_{init})}$
更に $M_1$ を利用して $\lambda_1 =\frac{\sum_{i=1}^M y_i}{M_1}$ を得られます。
※どうせポワソン分布以外から出てくるのは0なので、総和に変化はない。

また、 $\lambda_1$ を利用して $M_2$ を....といったようにそれぞれの数列
$M_1,M_2,\cdots$
$\lambda_1,\lambda_2,\cdots$
を得ます。

そして、 $\lambda$ の列が収束した段階で探索を止めます。

実例

シミュレーションデータ

prob=0.1
data=rpois(100000,lambda=1)*rbinom(100000,1,1-prob)

$\omega = 0.1,\lambda =1 , n=100000$

EMアルゴリズム

#lambda
init_lam=mean(data)
est_lam=init
alt_lam=100
#Mはポワソンから出ているサンプルの個数(潜在変数)
init_M=0
est_M=init_M
m=sum(data>0)
n=length(data)
S=sum(data)
while(abs(est_lam-alt_lam)>=0.001){
	alt_lam=est_lam
	est_M=m/(1-exp(-est_lam))
	est_lam=S/est_M
	if(abs(est_lam-alt_lam)<0.001){
		omega=1-est_M/n
	}
}

推定結果

> omega
[1] 0.09526407
> est_lam
[1] 0.9954507

かなり良い値が出てきましたね。

2019-01-14

Rで行えるロジスティック回帰に関するまとめ~最尤法、Penalized Likelihood (Firth)、ベイズ~

R Stan ベイズ統計学統計統計学基礎

今回はロジスティック回帰について、Rで出来ることを数式込みでまとめておきます。

ロジスティック回帰とは
最尤法
- モデル
- Rによるコード
Penalized Likelihood (Firth)
両者のシミュレーションによる比較
ベイズ
- Stanコード(普通の無情報事前分布)
- 無情報事前分布を与えた際の実行と結果
注意点
コメント
関連記事

ロジスティック回帰とは

最尤法

モデル

ロジスティック回帰は次のようなモデルです。

まず、1が出る確率 $Prob(Y_i=1|X_i)$ を次のように定義します。
$Prob(Y_i|X_i) = \frac{exp(\mu_i)}{1+exp(\mu_i)}$
$\mu_i = \beta_0+\beta_1 X_{\{1,i\}}+\cdots+\beta_k X_{\{k,i\}}$

要は、1が出るか0が出るかという確率の構造の中にXが関係していると考えます。

$i=1,2,\cdots,n$ とデータを取ってきたとするとその尤度 $l(\mu)$ は次のように得られるはずです。
$l(\mu)=\prod_{i=1}^n (\frac{1}{1+exp(\mu_i)})^{1-Y_i} (1-\frac{1}{1+exp(\mu_i)})^{Y_i}$

この尤度を最大化するパラメータの値を数値最適化を利用して探索的に(又は解析的に)求めます。

Rによるコード

Rではglm関数を利用してロジスティック回帰を簡単に行うことが出来ます。

glm(y~X1+X2+X3,family=binomial(logit))

familyにlogitであることを指定してやればOKです。

又は、optim関数を使って探索的に解を探すことも可能です。

fr=function(beta,X1,X2,X3,Y){
	sum(Y*(beta[1]*X1+beta[2]*X2+beta[3]*X3)-log(1+exp(beta[1]*X1+beta[2]*X2+beta[3]*X3)))
}

optim(c(0,0,0),fr,X1=X1,X2=X2,X3=X3,Y=y,method="BFGS",hessian=TRUE,control=list(fnscale=-1))

Penalized Likelihood (Firth)

数値的に 0 か 1 である確率が生じました

実際にglmを利用してロジスティック回帰をおこなっていると、時々次のようなエラーが出てきます。

数値的に 0 か 1 である確率が生じました

これ、何かというと、完全分離または準完全分離という状況が起こっている場合に出てくるエラーで、簡単に言ってしまうと、「現状のデータセットをモデルで完全に(又は境界を除いて完全に)予測出来てしまうようなケース」を指します。

この状況になると何が問題かというと、最尤推定を行った時に、値が一意にならず、探索する際の収束結果が安定しません。
つまり、推定結果がロバストではなくなります。

これは、ロジスティック回帰における小標本問題といって、まあもっとたくさん標本を取ってくれば解決するわけですが、これ以上標本を用意することはコスト的にも時間的にも厳しいという場合も多々あります。この場合にもいくつか改善策が提案されており、
・Exact logistic regression
・Penalized Likelihood logistic regression
などがあったりします。
※Exact logistic regressionを行うRパッケージは現状(2019年1月14日現在)無い。
一応elrmパッケージというものがあったっぽいけど、公式からremoveされているので、使わない方が良さげな気がする。

Penalized Likelihoodの方は、パッケージがあって、簡単に利用できるので、こっちを説明します。

この辺の詳しいpdfや論文は結構ネット上にあるので、リンクを貼っておきます。
https://www.jstor.org/stable/2336390
http://www.epistat.m.u-tokyo.ac.jp/admin/wp-content/uploads/2014/06/20140115tajima.pdf
http://www.applstat.gr.jp/jjas/V36N23_2.html
http://ir.c.chuo-u.ac.jp/repository/search/binary/p/4466/s/2278/

モデル

で、Penalized Likelihood logistic regressionですが、先ほどの最尤法で利用した尤度関数に対してフィッシャー情報行列を使って罰則を加えてやるモデルです。
フィッシャー情報行列 $i(\beta)$ を用いて
$l(\mu)+\frac{1}{2} log(|i(\beta)|)$

こうすることの利点は、まず完全分離においても安定した最尤推定値を出せるようになること、更に理論的にはExact logistic regressionに対する近似値を求めてることに等しく、ベイズの枠組みではジェッフェリーズ無情報事前分布を用いた推定と同値になります。

Rによるコード

Rでは、logistfパッケージに入っています。

library(logistf)

使い方はglmと同じでfirth=TRUEと指定してやればOKです。

logistf(y~0+X1+X2+X3,firth=TRUE)

両者のシミュレーションによる比較

データセット

とりあえず、サンプルサイズを1000から1000000まで1000刻みで動かして、その推定結果を見てみようと思う。

n_max=1000000
nseq=seq(1000,n_max,1000)
glmbeta1_seq=c()
glmbeta2_seq=c()
glmbeta3_seq=c()
firthbeta1_seq=c()
firthbeta2_seq=c()
firthbeta3_seq=c()
beta1=0.3
beta2=0.5
beta3=0.5
X1=sample((-50):50,n_max,replace=TRUE)
X2=sample(50:70,n_max,replace=TRUE)
X3=sample((-70):(-50),n_max,replace=TRUE)
mu=beta1*X1+beta2*X2+beta3*X3
probabl=exp(mu)/(1+exp(mu))
y=c()
for(p in probabl){
	if(p>=runif(1)){
		y[which(probabl==p)]=1
	}
	else{
		y[which(probabl==p)]=0
	}
}

大標本での結果

とりあえず推定。

for(i in nseq){
	res=glm(y[1:i]~0+X1[1:i]+X2[1:i]+X3[1:i],family=binomial(logit))
	glmbeta1_seq[which(nseq==i)]=coef(res)[1]
	glmbeta2_seq[which(nseq==i)]=coef(res)[2]
	glmbeta3_seq[which(nseq==i)]=coef(res)[3]
	res2=logistf(y[1:i]~0+X1[1:i]+X2[1:i]+X3[1:i],firth=TRUE)
	firthbeta1_seq[which(nseq==i)]=coef(res2)[1]
	firthbeta2_seq[which(nseq==i)]=coef(res2)[2]
	firthbeta3_seq[which(nseq==i)]=coef(res2)[3]
}

結果
f:id:bananarian:20190114114535p:plain

ほとんど同じ動きをしているっぽい。
真の値と微妙にズレているけど、係数比で見ると真の値に近くなっていることが確認出来ます。

値が安定してくるのがサンプルサイズ20000とか30000なのも気になりますね。実際のデータセットはかなり大規模なものでないとかなり誤差が大きくなりそう。

小標本での結果

Firthの手法が有用なのは小標本のケースなので、最大サンプルサイズ200でも試してみました。
結果はこんな感じ。

f:id:bananarian:20190114131618p:plain

Firthの方法は安定しているけど、普通の方法ではなんか変なとこに飛んでいってますね。

ベイズ

Stanコード(普通の無情報事前分布)

library(rstan)
model="
data{
	int<lower=1> N;
	int<lower=1> K;
	matrix[N,K] X;
	int<lower=0,upper=1> Y[N];
	
}

parameters{
	vector[K] beta;
}

transformed parameters{
	vector[N] mu;
	for(n in 1:N){
		mu[n]=beta[1]*X[n,1];
		for(k in 2:K){
			mu[n] = mu[n]+beta[k]*X[n,k];
		}
	}
}

model{
	Y ~bernoulli_logit(mu);
}
"

無情報事前分布を与えた際の実行と結果

データセット
サンプルサイズは10000で、さっきと同じようにデータを作ってみました。

n=10000
X1=sample((-50):50,n,replace=TRUE)
X2=sample(50:70,n,replace=TRUE)
X3=sample((-70):(-50),n,replace=TRUE)
beta0=0
beta1=0.3
beta2=0.5
beta3=0.5
sigma=sqrt(3)
mu=beta1*X1+beta2*X2+beta3*X3
probabl=exp(mu)/(1+exp(mu))
y=c()
for(p in probabl){
	if(p>=runif(1)){
		y[which(probabl==p)]=1
	}
	else{
		y[which(probabl==p)]=0
	}
}

data=list(N=length(y),K=3,X=cbind(X1,X2,X3),Y=y)

実行

fit=stan(model_code=model,data=data,seed=1234,pars="beta",chains=1)

結果

> fit
Inference for Stan model: ab047d734a690c818ea61b55250e593c.
1 chains, each with iter=2000; warmup=1000; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=1000.

            mean se_mean   sd     2.5%      25%      50%      75%    97.5% n_eff Rhat
beta[1]     0.22    0.00 0.01     0.21     0.22     0.22     0.22     0.23   285 1.01
beta[2]     0.37    0.00 0.01     0.35     0.37     0.37     0.38     0.40   233 1.01
beta[3]     0.37    0.00 0.01     0.35     0.37     0.37     0.38     0.40   230 1.01
lp__    -1468.07    0.07 1.09 -1470.91 -1468.59 -1467.81 -1467.25 -1466.76   265 1.00

Samples were drawn using NUTS(diag_e) at Mon Jan 14 14:09:11 2019.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

とりあえず、係数の大小関係は合っているので、オッズ比で考えれば問題なさそう。
小標本の時はpenalized likelihoodの理論的背景を元にジェッフェリーズ事前分布を与えた方が良いのかな？という感じですかね。

注意点

・ロジスティック回帰の係数を解釈する際は、パラメータの比でみる必要がある。つまり、例えば $\frac{\beta_2}{\beta_1}$ を見た場合、 $X_1$ の変化によって生じる選択確率への影響と、 $X_2$ の変化によって生じる選択確率への影響の比を見ていることになる。

・オッズ比による解釈が一般的。

・もし、係数を単独で解釈したいのであれば、全ての説明変数のスケールを揃えるために標準化してからパラメータを推定するか、次の線形モデルの形で解釈する必要がある。
$\log(\frac{p}{1-p})=\beta X$

・実際のモデリングにおいて、背後の生成過程はわからないので、確実に何かしらのノイズが発生するはず。具体的には次のような感じ。
$\mu = \beta X +\epsilon$
切片項を用意しても、このノイズには対応できないので、その辺どうすればいいのかが気になるけど、結局オッズ比で解釈することになるし、係数値の正確さは大小関係さえあっていればそんなに気にする必要はない？うーん。場合に寄りけり？でも、係数値を使わなければいけない場面では、その辺りに対応できるよう同時分布を考えた方が良いのかもしれないとも思いました。

Rで行えるプロビット回帰に関するまとめ~最尤法、ベイズ~ - バナナでもわかる話
 人間の選択をモデル化するプロビット・ロジットモデルの違いと経済学的解釈法 - バナナでもわかる話

2019-01-11

Rで行える線形回帰分析法の一覧とその方法~最小二乗法・最尤法・ベイズ~

R プログラミングベイズ統計学統計統計学基礎統計学雑記

今回は、線形回帰分析に関するRでの分析法を1記事にまとめておこうと思います。

線形回帰分析とは
シミュレーション用データ
最小二乗法
最尤法
ベイズ
３つの手法の比較
- 注意

線形回帰分析とは

今更感がありますが、一応線形回帰分析の説明をしておきます。
被説明変数(予測変数) $Y_i$ が説明変数 $X_{i,k}$ によって、次のような構造になっていると仮定します。

$Y_i =\alpha_0+\alpha_1 X_{i,1}+...+\alpha_K X_{i,K}+\epsilon_i$

ただし、
$\alpha_0,...\alpha_K$ は未知パラメータ
$\epsilon_i$ は誤差項(よってこれは確率変数)
$\epsilon_i$ は各々独立にある確率分布に従っているとする。
$Var[\epsilon_i]=\sigma^2$

この時、 $Y_i$ の条件付き分布 $Prob(Y_i|\alpha,\sigma,X)$ を考えておく。

この時の未知パラメータの推定量として妥当なものを様々な手法から検討したいというわけです。

シミュレーション用データ

適当に被説明変数 $Y$ と説明変数行列 $X$ を用意しておくことにします。

X1=sample(1:100,60,replace=FALSE)
X2=sample(30:50,60,replace=TRUE)
y=10+0.4*X1+5.2*X2+rnorm(60,0,sqrt(3))

サンプルサイズ $60$ ,誤差の分散が $\sqrt{3}=1.73$ のデータを使います。

最小二乗法

計算

最小二乗法は次のように計算します。
$Y=(Y_1,...Y_n)'$
$X=\begin{pmatrix} 1&X_{1,1}&\cdots&X_{1,K} \\ \vdots&\vdots&\ddots&\vdots \\ 1&X_{n,1}&\cdots&X_{n,K} \\ \end{pmatrix}$
$\alpha =(\alpha_0,\cdots,\alpha_K)'$
$\epsilon = (\epsilon_1,\cdots,\epsilon_n)'$

$Y=X \alpha +\epsilon$

といった形で行列表記すると、誤差は次のように表せます。
$\epsilon=Y-X \alpha$

よって誤差の二乗和は次のように表せます。
$\epsilon'\epsilon=(Y-X \alpha)'(Y-X \alpha)$

この誤差の二乗和を最小にするような $\alpha$ の値 $\hat{\alpha}$ を求めます。

$\epsilon'\epsilon=(Y-X \alpha)'(Y-X \alpha)=Y'Y-2Y'X \alpha+\alpha'X'X\alpha$
$\frac{\partial}{\partial \alpha}\epsilon'\epsilon=-2X'Y+2(X'X)\alpha$
$\hat{\alpha}=(X'X)^{-1}X'Y$

また、 $\sigma^2$ の不偏推定量 $\hat{\sigma}^2$ は
$\hat{\sigma}^2=\frac{(Y-X \hat{\alpha})'(Y-X \hat{\alpha})}{n-K}$

Rによる最小二乗法

Rで最小二乗推定値を求めるには、lm関数を利用します。

model1=lm(y~X1+X2)
n=length(y)
k=3
#係数の推定値を取り出す
a_hat1=coef(model1)
X=cbind(1,X1,X2)
#sigmaを計算する
sigma_hat1=t(y-X%*%a_hat1)%*%(y-X%*%a_hat1)/(n-k)

出力

> a_hat1
(Intercept)          X1          X2 
 10.2205439   0.4014095   5.1984349 
> sqrt(sigma_hat1)
         [,1]
[1,] 1.706484

実際の $\alpha,\sigma$ は
$\alpha_0=10,\alpha_1=0.4,\alpha_2=5.2,\sigma=1.73$
なので、そこそこ近い値が出ていることが分かります。

最小二乗法の特徴

・最小二乗法を使った推定量は、不偏性、一致性がある。更に、最良線形不偏推定量としても機能する。
・分布を仮定することなく、推定できる。

最尤法

計算

$\epsilon_i$ が正規分布に従っていると仮定します。
ここで、 $Prob(Y|\alpha,X,\sigma)$ は次のよう。

$Prob(Y|\alpha,X,\sigma)=(\frac{1}{\sqrt{2 \pi \sigma^2}})^n exp(-\sum_{i=1}^n \frac{(Y_i-X_{\{i,\}}\alpha)^2}{2\sigma^2})$

最尤法では対数尤度 $ln(Y;\alpha,X,\sigma)$ を取ると計算しやすいです。
$ln(Y;\alpha,X,\sigma)=log(Prob(Y|\alpha,X,\sigma))$
$=-nlog(2 \pi)-2nlog(\sigma)-\sum_{i=1}^n \frac{(Y_i-X_{\{i,\}}\alpha)^2}{2\sigma^2}$
$=-nlog(2 \pi)-2nlog(\sigma)-\frac{(Y-X \alpha)'(Y-X \alpha)}{2\sigma^2}$

対数尤度を最大化する $\alpha$ の値 $\hat{\alpha}_{ML}$ と $\sigma$ の値 $\hat{\sigma}_{ML}$ を求めたい。

$\frac{\partial}{\partial \alpha}ln(Y;\alpha,X,\sigma)=0$
$\frac{\partial}{\partial \sigma^2}ln(Y;\alpha,X,\sigma)=0$

を満たす値を求めればよく、計算してやると
$\hat{\alpha}_{ML} =\hat{\alpha} =(X'X)^{-1}X'Y$
$\hat{\sigma}_{ML}^2=\frac{(Y-X \hat{\alpha}_{ML})'(Y-X \hat{\alpha}_{ML})}{n}$

Rによる最尤推定

先ほどの計算式を打ち込んでみます。

a_hat=solve(t(X)%*%X)%*%t(X)%*%y
sigma_hat2=(t((y-X%*%a_hat))%*%(y-X%*%a_hat))/n

出力

> a_hat
         [,1]
   10.2205439
  0.4014095
  5.1984349
> sqrt(sigma_hat2)
         [,1]
[1,] 1.663275

係数の推定値は最小二乗法と同じですが、誤差の標準偏差の推定値が異なりますね。

最尤法の特徴

・最尤推定量は一致性を持つ
・漸近的に有効かつ不偏性を持つ
・分布を仮定する必要がある
・汎用性が高い

ベイズ

解説

ベイズではパラメータの事後分布 $P(\alpha_k|X,y),P(\sigma|X,y)$ を求めるか、その事後分布からのサンプリングを行うことでパラメータの分布を考えます。その際、推定値として何を採用するかが問題となってきます。事後平均、事後の中央値、最頻値等色々考えられます。
事前分布の選択も重要です。

Rstanによる実装(非ベクトル化編)

Stanによるモデリングを行います。
まず、普通にベクトル化せずに書いてみます。
Stanではパラメータに対して分布を設定しておかなかった場合、勝手に無情報事前分布が割り当てられます。

#パッケージ
library(rstan)
#モデル
model2="
data{
	int N;
	int K;
	real X[N,(K-1)];
	real Y[N];
}

parameters{
	real a[K];
	real<lower=0> sigma;
}

transformed parameters{
	real mu[N];
	for(n in 1:N){
		mu[n]=a[1];
		for(k in 2:K){
			mu[n]=mu[n]+a[k]*X[n,(k-1)];
		}
	}
}

model{
	for(n in 1:N){
		Y[n] ~ normal(mu[n],sigma);
	}
}
"
data_list=list(N=n,K=k,X=cbind(X1,X2),Y=y)
fit=stan(model_code=model2,data=data_list,seed=1234)

出力

> fit
Inference for Stan model: c126dea47c42ac03e7ce323de93ea362.
4 chains, each with iter=2000; warmup=1000; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=4000.

         mean se_mean   sd   2.5%    25%    50%    75%  97.5% n_eff Rhat
a[1]    10.26    0.04 1.66   6.95   9.17  10.28  11.40  13.47  1487    1
a[2]     0.40    0.00 0.01   0.38   0.40   0.40   0.41   0.42  2709    1
a[3]     5.20    0.00 0.04   5.12   5.17   5.20   5.22   5.28  1502    1
sigma    1.74    0.00 0.17   1.45   1.62   1.73   1.85   2.11  2438    1

今回は事後平均を推定値として採用するとします。
この場合推定値は $\hat{a_0}_{Bayes}=10.26,\hat{a_1}_{Bayes}=0.40,\hat{a_2}_{Bayes}=5.20,\hat{\sigma}_{Bayes}=1.74$

より効率の良いコード(ベクトル化編)

Stanはベクトル化した方が計算速度が速くなることがあります。
ベクトル化したコードをもう一度書いてみます。

model3="
data{
	int N;
	int K;
	matrix[N,K] X;
	vector[N] Y; 
}

parameters{
	vector[K] a;
	real<lower=0> sigma;
}

transformed parameters{
	vector[N] mu;
	mu = X*a;
}

model{
	Y~normal(mu,sigma);
}
"

data_list2=list(N=n,K=k,X=X,Y=y)
fit2=stan(model_code=model3,data=data_list2,seed=1234)

計算速度を調べるためにはproc.time関数を使います。

t=proc.time()
fit=stan(model_code=model2,data=data_list,seed=1234)
proc.time()-t

t=proc.time()
fit2=stan(model_code=model3,data=data_list2,seed=1234)
proc.time()-t

model2の出力

> proc.time()-t
   ユーザ   システム       経過  
      3.92       0.56       4.59

model3の出力

> proc.time()-t
   ユーザ   システム       経過  
      3.55       0.17       3.80

経過時間がmodel3の方が早くなっていることが確認出来ます。

ベイズの特徴

・最尤法の一般化概念と捉えることも出来る
・最尤法との違いは、最尤法はmonotonicな変数変換に対して不変なのに対して、ベイズは事後平均等を用いるため変化してしまう
・階層モデル等に拡張することも出来る
・事後の条件付き分布を見ているにすぎないことに注意

３つの手法の比較

実際は背後の真のパラメータの値によりけりなので、それぞれの特徴を考慮した上で方法を選ぶことになるわけですが、今回はシミュレーション出来るので、サンプルサイズを変えて比較してみました。

N=10:300
a0=10
a1=0.4
a2=5.2
sigma=sqrt(3)
a0hat1=c()
a1hat1=c()
a2hat1=c()
a0hatB=c()
a1hatB=c()
a2hatB=c()
sigmahat1=c()
sigmahat2=c()
sigmahatB=c()

for(nn in N){
	X1=sample(1:1000,nn,replace=FALSE)
	X2=sample(300:500,nn,replace=TRUE)
	y=a0+a1*X1+a2*X2+rnorm(nn,0,sigma)
	model1=lm(y~X1+X2)
	n=length(y)
	k=3
	X=cbind(1,X1,X2)
	a0hat1[which(N==nn)]=coef(model1)[1]
	a1hat1[which(N==nn)]=coef(model1)[2]
	a2hat1[which(N==nn)]=coef(model1)[3]
	sigmahat1[which(N==nn)]=sqrt(t(y-X%*%a_hat1)%*%(y-X%*%a_hat1)/(nn-k))
	sigmahat2[which(N==nn)]=sqrt(t(y-X%*%a_hat1)%*%(y-X%*%a_hat1)/nn)
	data_list2=list(N=n,K=k,X=X,Y=y)
	fit2=stan(model_code=model3,data=data_list2,seed=1234,chains=1)
	sigmahatB[which(N==nn)]=mean(rstan::extract(fit2)$sigma)
	a0hatB[which(N==nn)]=mean((rstan::extract(fit2)$a)[,1])
	a1hatB[which(N==nn)]=mean((rstan::extract(fit2)$a)[,2])
	a2hatB[which(N==nn)]=mean((rstan::extract(fit2)$a)[,3])
}

par(mfcol=c(2,2))	
plot(N,a0hat1,xlab="sample size",ylab="",main="a0",col="red",type="l")
points(N,rep(a0,length(N)),col="black",type="l")
points(N,a0hatB,col="green",type="l")
legend("topright", legend = c("OLS","Bayes"), col = c("red","green"),lty=c("solid","solid"))

plot(N,a1hat1,xlab="sample size",ylab="",main="a1",col="red",type="l")
points(N,rep(a1,length(N)),col="black",type="l")
points(N,a1hatB,col="green",type="l")
legend("topright", legend = c("OLS","Bayes"), col = c("red","green"),lty=c("solid","solid"))

plot(N,a2hat1,xlab="sample size",ylab="",main="a2",col="red",type="l")
points(N,rep(a2,length(N)),col="black",type="l")
points(N,a2hatB,col="green",type="l")
legend("topright", legend = c("OLS","Bayes"), col = c("red","green"),lty=c("solid","solid"))

plot(N,sigmahat1,xlab="sample size",ylab="",main="sigma",col="red",type="l")
points(N,rep(sigma,length(N)),col="black",type="l")
points(N,sigmahatB,col="green",type="l")
points(N,sigmahat2,col="yellow",type="l")
legend("topright", legend = c("OLS","Bayes","MLE"), col = c("red","green","yellow"),lty=c("solid","solid","solid"))

出力はこんな感じ。
f:id:bananarian:20190111002223p:plain
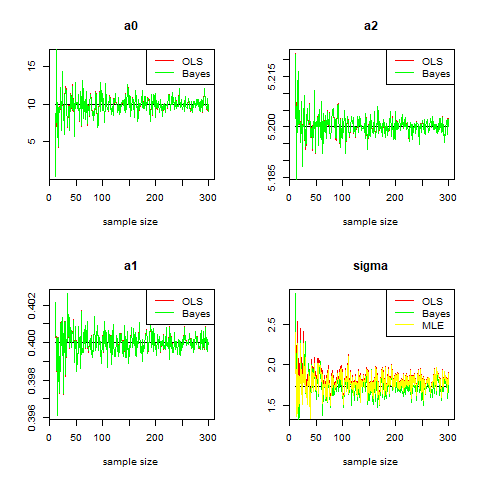
$\sigma$ の推定値が推定方法によって収束スピードが異なっている様子が見て取れます。

試しにもう少し比較してみると

par(mfcol=c(2,2))
plot(N,sigmahat1,xlab="sample size",ylab="",main="sigmaOLS",col="red",type="l",ylim=c(1,3))
points(N,rep(sigma,length(N)),col="black",type="l")
plot(N,sigmahat2,xlab="sample size",ylab="",main="sigmaMLE",col="red",type="l",ylim=c(1,3))
points(N,rep(sigma,length(N)),col="black",type="l")
plot(N,sigmahatB,xlab="sample size",ylab="",main="sigmaBayes",col="red",type="l",ylim=c(1,3))
points(N,rep(sigma,length(N)),col="black",type="l")

f:id:bananarian:20190111003111p:plain

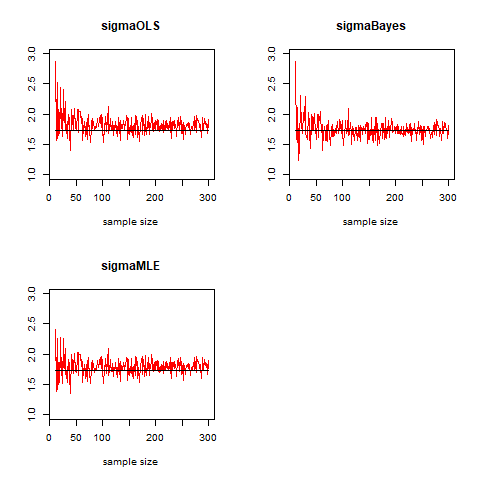
プロットをした印象としては、ある程度サンプルサイズの大きくなると、事後分布からの事後平均を使ったものが安定していそうな気がします。
真の値との誤差も求めてみます。

今回求めた全ての推定値から誤差を求めた場合

> sum((sigmahat1-sigma)^2)
[1] 9.220136
> sum((sigmahat2-sigma)^2)
[1] 6.285238
> sum((sigmahatB-sigma)^2)
[1] 6.807877

最尤推定量を使った値が最も誤差の総和が小さい

一方、サンプルサイズが50より大きい所で見た場合

> sum((sigmahat1[40:length(N)]-sigma)^2)
[1] 4.474911
> sum((sigmahat2[40:length(N)]-sigma)^2)
[1] 3.742564
> sum((sigmahatB[40:length(N)]-sigma)^2)
[1] 3.059328

ベイズ事後平均が最も誤差の総和が小さくなっています。

よって、今回の場合、高々サンプルサイズ300程度の推定では、誤差項の標準偏差はベイズ事後平均を使うのが良かったということになりました(結果論ですが。)

注意

・まず、線形回帰分析の場合はベイズを使えといった類の話ではありませんので、注意してください。今回のケースを試しに1回の実験で比較してみたら、偶然ベイズが勝ったというそれだけの話です。

・今回の比較は少々不偏推定量には都合の悪い物だったようにも思います(不偏推定量は平均的に真の値に近づく)

・正直、各サンプルサイズごとに1回こっきりの推定しかしていないので、各サンプルサイズにおいて何度も推定を行って比較を行うと、また話が変わるような気がします(多分サンプルサイズが小さいところでは、不偏推定量が勝つような気がする)。

2019-01-09

サービスの4つの特性と統計モデリングでの注意点

マーケティングリサーチ経済学統計

今日は、有名なサービスの4特性を通じて、サービスに関するデータ解析で注意すべき点を記事にしようと思います。

サービス

まず、サービスとはという話ですが、例えばコンビニや銀行、ファミレス等での接客や企業に対するコンサルタント、美容院のカットなどを指します。

※経済経営学部に入るとまず初めに「サービス」と「製品」という商品の区別を教わりますが、製品とは私たちがすぐ想像するところの商品のことだと思ってもらって問題ないかと思います。例えばテレビやスマホ、冷蔵庫などといった形があるような商品のことですね。

サービスの性質

無形性

まず、サービスと製品の大きな違いに「無形性」があります。
その名の通りサービスは製品と違って物質的な性質が無い、簡単に言ってしまえばサービスには形がないということを指しています。

「そんなのあたりまえじゃないか！」と思うわけですが、これは意外と重要な性質で、

まず、形が無いので顧客が事前にその内容や質をチェックすることが出来なく(難しく)なります。

例えばこれが製品であれば、掃除機を買いたいから実際の店舗で吸引力を比較するだとか、マッサージチェアの購入検討のために電気屋さんで30分ほど試しに使ってみるなんてことが出来るわけですし、ニ〇リでお皿を購入したいとなれば、実店舗で手にとってその質感や色み等々を確認することが出来ます。

一方これが例えばある企業がコンサルタント会社さんに新しい事業に関する戦略を立ててもらうことになったとして、そのコンサルタントの質は実際にそのサービスを購入し、消費しない限りわかりません。何故なら形がなく、事前のチェックが不可能だからです。

他にも例えば、福岡県に旅行に行こう！となってホテルを予約するとします。このホテルが実際どのようなサービスを提供してくれて、どの程度の質かは実際に泊まってみないとわかりませんよね。

この意味で、サービスと製品は明確に性質が異なるわけです。
故に、一般に顧客にとっては「製品を購入することよりも、サービスを購入することの方がリスキー」に感じるわけです。
これを、顧客の知覚リスクと呼びます。

そのためサービスを提供する企業は顧客の知覚リスクの低減を目的に、例えばホテル会社であれば自社のホテルの内装やサービス内容などをホームページ上に公開したり、権威ある賞や資格を保有していることを示したりするわけです。学習塾などであれば体験入塾制度なんてのもありますよね。

同時性

次にサービスの同時性という性質について説明します。
同時性とは、生産と消費がほとんど同時に発生するという性質を指します。

製品でこれはまず起こりませんよね。工場で作られた冷蔵庫が作られた瞬間使用され始めるなんてことはないはずです。

一方、ファミレスの接客なんかを考えると、店員は実際にお客さんと関わることで初めて接客を行います。つまり生産を行うわけです。そしてそれと同時にお客さんは店員の接客を受けることで消費していますよね。

このような性質をサービスの同時性と呼んだりします。

異質性

製品は、工場で規格を管理しておけば、たまに不良品は出るかもしれませんが、ほとんど同じ質の商品が出来上がります。

一方でサービスはかなり対応するサービス提供者ありきのものになります。これをサービスの異質性と呼びます。
これを管理するのは中々難しいわけですが、極力同じになるよう事前研修を徹底したりするわけですね。

消滅性

普通製品は、在庫管理を行います。ちょっと多めに作っておいて注文が入る度に出荷するなんてことをよくやるわけですが、
サービスに関してはそんなことは出来ません。

生産と同時に消滅するのがサービスです。これを消滅性と呼んだりします。
これがサービス提供の難しい所で、サービスは生産(コストとして発生)されていても、消費が伴わない場合があり得ます。
具体的に言うと、客の入らない美容院だと、美容師の給料は時給単位で発生しているのに、お客はこないからコストだけが増えるとかそういう話です。

統計解析における注意点

無形性

顧客はサービスを購入する際、リスクを極力減らすために数々の情報を利用して、購買行動を決定します。
例えば初めて入る飲食店の口コミを事前に調べておくだとか、価格帯からそのサービスの質を推定するといった行動です。

そして、そうした情報を元に購買を決定するわけですが、この際顧客の購買行動をモデリングするにあたっては次のような問題点があります。

1. 使用経験とマーケティング変数
まず、初回の購買において、口コミ等の情報を集めたりするのはそうですが、例えばラーメン屋A、ラーメン屋Bのどちらを選ぶかといった場合に、ラーメン屋Aはネットの情報しか得られないが、ラーメン屋Bは一度実際に行ったことがあり、「おいしいかった」という経験的な事実があるとします。この場合、「今日は確実においしいラーメンを食べたい」と思えば、ネット上の情報は頼りにせず(というか、見ることもせず)、一度入ったことのあるラーメン屋Bに入るはずですし、今回は「比較のためにラーメン屋Aに入ってみるか」と思うかもしれません。

つまり、マーケティング変数は、顧客の初期購買の行動分析においては信用たり得ますが、それ以降の購買は使用経験が影響を及ぼしている可能性が高く、マーケティング変数だけでは説明出来ない結果になりやすいということになるわけです。

2. リスクの顧客依存
また、どの程度サービスの不透明さに対してリスクを感じるかは当然顧客に依存します。
全くリスクに感じない人であれば、何も調べず、何の情報もなくサービスを購買することもあるかもしれません。

「髪さえ切ってもらえればどこでもいいや」

なんて考えて適当に美容院を選んでいる男の人とかはそんな感じかもしれません。
こんな感じの顧客であれば、価格帯だけを見てあとは自分の家に近いかどうかでサービスを選ぶなんてこともしているかもしれませんよね。

同時性

1. 顧客と提供者の相互関係
サービスは、サービス提供者と顧客が同じ場所に居合わせるという少々特殊な商品です。
そのため、当然サービス提供者と顧客の相互作用も発生していると考えられます。
その相互作用の結果が事後的なサービス品質の評価に影響し、リピート購買に繋がるかが変わって来ている可能性も否めません。

異質性

1. サービス提供者の質
サービスの異質性を考えれば、当然サービス品質はそのサービス提供者による影響が大きいと言わざるを得ません。
そのため、単純なモデリングで異質性を排してしまうと実態にそぐわない結果を導く恐れがあります。

このように、サービスは普通の製品とは大きく異なり、実際にサービス関連のモデリングをするにあたっても複雑なモデルを作ってやる必要が生じます(当然、得られているデータのサンプルサイズとの兼ね合いも考えた上で、妥協するところは妥協する。)

2019-01-03

Rのplotを使ってNealの漏斗を可視化してみる

Stan R ベイズ統計学機械学習統計

今日は、「StanとRでベイズ統計モデリング」という本の10章にあるNealの漏斗問題の可視化を簡単なコードだけで行ってみたいと思います。

ちなみにStanとRでベイズ統計モデリングとは、こちらの本です。
<br />

こちらの本、全てのコードがしっかりサポートページに掲載されていて、とても勉強になるのですが、10章にあるNealの漏斗の図は省略されていて(私が見た限り載っていなくて/2019年1月3日現在)、どうやって可視化すればいいんだろうと思ったのでやってみました。
とりあえず、綺麗な図というよりは確認出来ればいいので簡単なplotで試してみたいと思います。

Nealの漏斗問題

まず、Nealの漏斗問題とは何かというと、ベイズモデルを作った際に、パラメータ同士対数事後周辺尤度が次のような漏斗状の形になることで生じるサンプリング問題を指します。
f:id:bananarian:20190103152542p:plain

このような状況になると、愚直にStanでモデリングを行っても、サンプルを効率よく取ってくることが出来ません。そこで再パラメータ化という、一旦独立な分布からサンプリングしてやったのち、変数変換を行う処置をとるわけです。

Rコード

では、コードを打っていきます。

まず、rstanの読み込み

library(rstan)

次にモデルを作っておきます

model="
parameters{
	real a;
	vector[1000] r;
}

model{
	a~normal(0,3);
	r~normal(0,exp(a/2));
}"

fit_a=stan(model_code=model,seed=1234,chains=1,iter=4000)
a1=rstan::extract(fit_a)$a
r1=rstan::extract(fit_a)$r[,1]

この状態でのサンプリングはあまりうまくいきません。それをplotでチェックします。

r=seq(-10,10,0.025)
a=seq(-10,10,0.025)
n=length(r)
lp1=matrix(,n,n)
for(i in r){
	for(j in a){
		lp1[which(r==i),which(a==j)]=log(dnorm(i,0,3))+log(dnorm(j,0,exp(i/2)))
	}
}
lp1[lp1==-Inf]=0
contour(r,a,t(lp1))
points(r1,a1,col="red")

f:id:bananarian:20190103153136p:plain

あまりうまくサンプリング出来ていないことが確認出来ました。

さて、再パラメータ化を行った場合はどうでしょう。

model2="
parameters{
	real a_raw;
	vector[1000] r_raw;
}

transformed parameters{
	real a;
	vector[1000] r;
	a=3.0*a_raw;
	r=exp(a/2)*r_raw;
}

model{
	a_raw~normal(0,1);
	r_raw~normal(0,1);
}"

fit_b=stan(model_code=model2,seed=1234,chains=1,iter=4000)
a2=rstan::extract(fit_b)$a
r2=rstan::extract(fit_b)$r[,1]

重ねてみる

contour(r,a,t(lp1))
points(r2,a2,col="green")

f:id:bananarian:20190103153354p:plain

漏斗の先も取ってきて来れていることが確認出来ました！

2018-12-26

次元削減とは

統計機械学習

今日は統計学や機械学習、その他画像認識等の場面で登場する「次元削減」の話について書こうと思います。

まず、次元削減とは、 $n$ 次元データを $n-k$ 次元にうつすことで、次元を下げることを指します。

簡単に例を出すと、
例えば国語・数学・理科・社会の4科目(1科目0点~100点)のテストをしたとします。
この時太郎君は国語:70点、数学:90点、理科:85点、社会:60点だったとします。

今現在変数は４つあって、
国語の得点(0点~100点)
数学の得点(0点~100点)
理科の得点(0点~100点)
社会の得点(0点~100点)となってるわけですが、

太郎君の点数を見た塾の先生や、太郎君の親は

「太郎君は、理系科目が得意だね～」

なんて言ったりしますよね。

でも、今ある変数に「理系科目変数」なんてものは無いわけです。
当たり前ですが、これは次のようなプロセスで導かれています。

国語・社会⇒文系科目
数学・理科⇒理系科目

と置き換え、
(文系科目)<(理系科目)という何かしらの基準に基づく大小関係を考え、「太郎君は理系科目の方が得意」という話になるわけです。

特に数学や国語に重きを置くわけでないのなら、例えば次のような変換が出来ますね。
$X_{国語},X_{社会},X_{数学},X_{理科}$ という得点変数について、

$Y_{文系科目}=\frac{1}{2}X_{国語}+\frac{1}{2}X_{社会}$
$Y_{理系科目}=\frac{1}{2}X_{数学}+\frac{1}{2}X_{理科}$

今回であれば太郎君の $Y_{文系科目},Y_{理系科目}$ は次のようになるはずです。
$Y_{文系科目} =65$
$Y_{理系科目} =87.5$

つまり、 $Y_{文系科目}$ < $Y_{理系科目}$ で、太郎君は理系科目の方が得意だとなるわけです。

この簡単な変換も実は「次元削減」です。

4次元(国語・数学・理科・社会)あったデータが2次元(文系科目・理系科目)になっていますよね。

この次元削減、どんな利点があるのでしょう。
何の利点も無いのに、人間が普段の会話で何となくこんな次元削減したりすることはないはずです。

一番の理由は多次元空間の解釈の難しさにあります。
国語・数学・理科・社会ならまださておき、8科目、9科目、かなり細かい専門に分けて10科目以上のテストをしたとして、その人の特性をどう解釈したらよいでしょうか。生データのままでは、せいぜい「この科目よりこの科目の方が点数が高い」とかそれくらいしか言えません。

結局色々なデータがあっても、多次元すぎてどう解釈すればわかりませんねーとなるわけです。

そこで、有用な情報を残したまま(あまり差の出ない情報は捨てて)、解釈しやすい次元までデータを持って行ってやろう！

となるわけですね。これが次元削減です。

しかし、有用な情報を残すとは具体的にどういうことでしょう。
先ほどの例は、国語と社会は文系科目という分類が一般認識としてあるので、次元削減の方法までは考える必要もありませんでしたが、実データでは、「削減したいのはやまやまだけど、どう分けたらいいか分からない！」という状況の方が多かったりします。

そこで普通は(色々方法はありますが、よくある手法として)、データの分散に着目するわけですね。
主成分分析や決定木等の手法は、分散に着目した分析法です。

何故分散に着目するかというと、話は単純で

分散が小さい⇒データ間に決定的に差が無い

と考えられるからです。
例えば10人生徒に対して、国語のテストをしたとします。点数が次のようになったとすると
$10,11,23,21,5,90,89,95,99,100$
国語の得意な生徒と苦手な生徒に分けるのは簡単ですね。つまりこのデータには、国語の得意・苦手の情報がしっかり入っているため、国語が得意か苦手か分けることが容易ということになります。

点数が次のようになっていたとすると
$76,70,69,71,77,83,65,72,72$
これで国語の得意な生徒と苦手な生徒に分けるのはしんどそうです。
つまり、このデータは分散が小さく、皆が似通った点数を取っているため、国語の得意な生徒と苦手な生徒に分けるのは難しいということになります。

もしかしたら、生徒皆が国語のテストが得意で、全国平均20点のテストを受けているのかもしれませんし、実は生徒皆が国語のテストが苦手で、全国平均90点のテストを受けてこの点数になっているかもしれません。また、70点くらいまでならだれでも取れるけど、それ以上を取るのが難しいようなテストで、得意な人も苦手な人も点数が均されている可能性もありますね。

何が言いたいかというと、分散が小さい分類基準よりも、分散が大きい分類基準の方が、そのデータの性質が見出されやすいということです。

だから、特に主成分分析では、分散が大きくなるように主成分を決定していきますよね。

これが、次元削減の概要になります。
また次回にでも主成分分析等々の手法について記事をあげていこうと思います。

2018-12-21

一様事前分布は無情報ではないという話

ベイズ統計学統計

ベイズで何かを議論する際に、よく無情報事前分布として一様分布が用いられます。
何をもって""無情報""と呼ぶかっていうのは難しい問題で、今回はその話をしようと思います。

まず、一様分布ってのは要は平坦な分布だと思ってください。

で、平坦な分布を取るってどういうことかというと、範囲が0から1を取るパラメータ $\theta$ を考えたとすると、 $\theta$ に対して与えられる確率分布は下のように値1で平坦になるはずです。
f:id:bananarian:20181220232751p:plain

これが要は一様分布です。直感的には情報なんてないような気がします。
だって取りうる値の範囲で等確率を取っていて、何か一つの値が出やすいわけでも無いので、直感的には対等だというわけです。

でも、これには欠点があって、パラメータの形を「 $\theta$ 」と決めつけている所に情報があります。

何を言っているかというと、別にパラメータとして $\theta$ ではなく、 $exp(\theta)$ を考えても良いのでは？ということです。

ちなみに $exp(\theta)$ という形に変換してやった時の一様分布は次のようになります。
f:id:bananarian:20181220233429p:plain

範囲と高さが変わっているのわかりますかね？
何が言いたいかというと、「パラメータをどう見るか」を分析者は無意識に決定していて、その時点で少しばかり偏見が入っている。その意味で無情報と呼ぶべきではないという立場が存在するということです。

具体例を挙げると、例えば次のような線形モデルを考えます。
$y=\beta X +\epsilon$

この時、別に次のように見て、パラメータ $exp(\theta)$ を考えても良いわけです。
$y = log(exp(\beta)) X +\epsilon$

そんな難癖どうやって解決すればいいんだ！！というと、
実はこの変数変換問題を解決できる事前分布が存在してジェフェリーズの事前分布と呼ばれています。

まあ、そうそうこんな難癖をつけてくる人はいないでしょうが、当然もし難癖をつけられた時の為に色々な事前分布は知っておいた方が良さそうです。次回は、ジェフェリーズの事前分布について説明しようと思います。

それではまた次回。

2018-12-15

順序選択モデルの数理と解釈~ベイズモデルの構成法~

経済学統計マーケティングリサーチベイズ統計学

今日は順序選択モデルというモデルについて書くことにします。

具体例

例えば焼肉屋さんで、ライスを頼みたいと思ったとします。
この時に小ライスか、中ライスか、大ライスが選べるとします。

これ、この順序選択モデルを知らない人だと真っ先に「多項選択モデルを当てはめてみよう」という思考になるはずです。

そんでもって小ライスを0,中ライスを1,大ライスを2として、その選択を考えることになります。

しかし、これは少し不自然で、例えばこれがカルビを選ぶかサガリを選ぶか、それともミノを選ぶかみたいな選択だと0,1,2と割り当てれば良いわけですが、今回って選択肢に順序がありますよね。 小ライス＜中ライス＜大ライス といった具合です。

この場合何が起こるかというと、量に順序があるということは、人間の選択に順序が影響し始めます。
「今は小腹が空いている程度だから、大ライスは頼めないなー」なんて考えて、大ライス未満の順位にあるライス、つまり中ライスか小ライスを選択するだとか、「とてもお腹が空いているから小ライスや中ライスのような下の順位のライスではなく、大ライスを頼もう」なんて考えたりだとか。

そういった状況なのだから、モデルを使うにあたっても順序を考慮したモデルを考えた方がより状況を反映した結果が得られるはずです。

「ん？0,1,2を割り当てた時点で、数字上0が1番小さくて2が1番大きいのだから、順序は考慮できているのでは？」

と思う方もいらっしゃるかもしれませんが、これは少々まずくて、数字上の距離を仮定してしまっています。
どういうことかというと、要は小ライスと中ライスの距離、中ライスと大ライスの距離が1であり、小ライスと大ライスの距離が2であるという仮定のもと大小を決めていますよね。量的変数ならまだしも、質的変数でこの仮定はあまり説得力がありません。